Пусть даны 2 комплексных числа 
, 
Сумма двух компл. чисел –комплексное число 
. Разность: 
Произведение: 
Св-ва:
(коммутативность) 
, , 
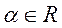
сущ-ет нейьральный элемент 
, такой, что 
сущ-ет единичный элемент 
, такой, что 
,
Для любого 
сущ-ет такой элемент 
, что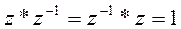 
з-н ассоциативности: 
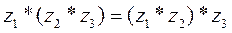
-ной степенью компл. числа 
наз комплексное число 
Деление компл. чисел: 
Пр. 
Лемма
Тригонометрическая форма комплексного числа. Пусть 
и даны прямоуг. и номерная с-ма координат, тогда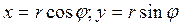 
. Тогда 
–тригонометрич. форма.
Переход от алгебраической формы к тригонометрич. осущ-тся по ф-ле: 
,
Теорема. Пусть комплексные числа 
и 
заданы тригонометрич. формой 
, тогда 
Следствие: 
Пр. 
Извлечение корня из комплексного числа
Корнем –ной степени, 
из компл. числа 
наз комплексное число 
, для к-рого 
. обознач. 
.
Алгебраическое ур-ние –ной степени над полем комплексных чисел имеет ровно корней – ф-ла Муавра. Корень –ной степени из комплексного числа 
, записанного в тригонометрической форме вычисляется по ф-ле
Вопрос №36.Дифференциальные ур-ния.
ДУ наз соотношение, связывающее независимую переменную 
, искомую ф. 
и ее производную. Если искомая ф. есть ф-я одной независимой переменной, то ДУ наз обыкновенным. Порядок старшей производной, входящей в ДУ наз порядком данного ур-ния.
Общий вид ДУ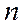 
–ного порядка 
. (1)
Ф-ия y=f(x), кот-я при подстановке в ур-е (1) обращает этоур-е в тождество, наз-ся решением этого ур-я.
ДУ 1-го порядка имеет вид: F(x,y,y’)=0 (2) или y’=f(x,y)(3) в случае, если y’ можно выразить относительно x и y
Реш-е ур-я (3) наз-ся общим реш-ем этого ур-я.
Реш-е может получаться в неявной форме Ф(x,y,c)=0 – наз общим интегралом.
Реш-е, кот получается из общего при некотором фиксированном значении С наз частным решением. Условия, что при x=x0 ф-ия y=y0 наз начальным условием, кот-е позволяет из общего реш-я выделить частное.
Ур-я с разделяющимися переменными.
Ур-е вида 
наз ур-ем с разделяющимися переменными. Это ур-е можно записать в виде: 
, домножим на 
:
Вычислим: 
Однородные ДУ
Ф-ия f(x,y) наз однородной измерения М если имеет место тождество f(xt,yt)=tm(x,y)
f(x,y) = x2-3xy+2y2
f(tx,ty)=(tx)2-3(tx)(ty)+2(ty)2=t2(x2-3xy+2y2)=t2f(x,y) – однородная ф-ия измерения t.
Ур-е M(x,y)dx+N(x,y)dy=0 наз однородным ДУ 1-го порядка, если ф-ии M и N однородные ф-ии одного и того же измерения.
С помощью подстановки y=ux, где u – искомая ф-ия, зависящая от x, ур-е сводится к ур-ю с разделяющимися переменными.
Линейные ДУ 1-го порядка: Ур-е вида y’+p(x)y=q(x)
Для реш-я исп-ют подстановку y=uv; dy=vdu+udv
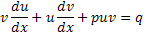
Ф-ию 
подбирают т.о., чтобы 
=0.
Метод Лагранжа.
Линейное ДУ 1-го порядка наз линейным если 
Y’+py=0
Для ур-й 1-го порядка это ур-е с разделяющимися переменными. Метод Лагранжа заключается в следующем: сначала мы решаем соответственно однородное ур-е, полученная ф-ия содержит С. Для реш-я исходного ур-я подбираем С т.о., чтобы реш-е однородного ур-я давало реш-е исходного, считая С зависящей от x.
ДУ второго порядка
Общий вид: F(x,y,y’,y’’)=0. Общее реш-е содержит 2 независимые произвольные постоянные с1 и с2. Если заданы начальные условия y(x0)=y0, y’(x0) = y’0, то из с-мы 
можно найти произв постоянные с1 и с2, тем самым найти частное реш-е 
Ур-я 2-го порядка решаются путём применения неопределённого интегрирования в след случаях:
1. Пусть 
; 
; 
;
; 
+c
2. 
Положим 
, тогда 
=> данное ур примет вид: 
, те получаем ур 1-го порядка с разделяющимися переменными.
Однородные линейные ДУ 2-го порядка имеет вид: 
; p,q – нек действительные числа.
Искать решение в виде 
λ2+pλ+q=0 – характеристическое ур-е.
1 случай: ур-е имеет 2 действит корня, λ1≠ λ2, тогда общее реш-е имеет вид: 
2 случай: ур-е имеет 2 действит совп корня λ1= λ2= λ
Общее реш-е: 
3 случай: корни квадратного ур-я мнимые: λ1,2= 
,
Общий вид: 
Линейные неоднородные ДУ 2-го порядка с постоянными коэффициентами: 
Т. Общее реш-е неоднородного ЛДУ 2-го порядка с пост коээф-ми равно 
решения соответствующего однородного ур-я и частноо реш-я исходного неоднородного ур-я.
Нахождение частного реш-я неоднородного ур-я:
1. Пусть правая часть – показательная ф-ия, 
a≠0:
а) m не явл корнем характеристического многочлена, тогда частное реш-е в виде: 
б) если характеристическое ур-е имеет 2 разл действ корня, один из кот-х = m, то частное реш-е в виде: 
в) если корни характеристического ур-я совпадают и равны m, то частное реш-е в виде: 
2. Правая часть неоднородного ур-я – тригонометрическая ф-ия 
Частное реш-е в случае, когда ± ki не явл-ся корнем характеристического ур-я 
Если же ki явл корнем хар-го ур-я, то частное реш-е в виде: 
3. Правая часть линейного ур-я предст собой многочлен Pn(x), тогда частное реш-е в случае когла q≠0 будем искать в виде Qn(x)
Если q=0, p≠0, тогда в виде xQn(x).
