Пусть ф-я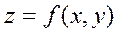 
определена в нек-рой области 
и пусть 
. Т.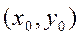 
наз точкой максимума ф-и 
, если существует такая D– окрестность т. 
, что для любой точки из этой окрестности вып-тся нер-во 
< 
. Аналогично определяется т. минимума. Для всех точек из D– окрестности 
> 
значение ф-и в точке максимума (минимума) наз максимальным (минимальным) значением или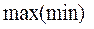 
. 
называют экстремумом.
В силу определения т. экстремума лежит внутри области определения ф-и. 
имеют локальный хар-р. В области определения ф-я может иметь неск-ко экстремумов.
Т. Необходимое условие экстремума. Если в точке 
дифференцируемая ф-я 
имеет экстремум, то в этой точке частные производные =0.
О. Точка, в к-рой частные производные =0 наз стационарной. Стационарные точки, а также точки, в к-рых хотя бы одна из частных производных не существует наз-ют критическими. Для нахождения точек экстремума необходимо каждую критическую точку в области определения подвергнуть доп. исследованию.
Т. Достаточное условие экстремума. Пусть стационарные точки 
и нек-рой ее окрестности ф-я 
имеет непрерывные частные производные до 2-го порядка включительно. Вычислим в точке 
значение
Составим определитель 
. Тогда 1)если D>0, то в т. 
–экстремум. Причем, если А<0 – максимум, если А>0–минимум. 2)Если D<0, то ф-я в т. 
экстремума не имеет. 3)В случае, когда D=0, экстремум в ф-и может быть, а может и не быть.
Вопрос №33.Понятие двойного и тройного интеграла.
Двойной интеграл и его св-ва.
Двойным интегралом от ф-и 
по области 
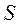наз предел ее интегральной суммы при l®0, т.е. 
Ф-я –наз подинтегральной ф-ей. 
–область интегрирования, 
также обозначается 
. Если предел сущ-ет, то ф-я наз интегрируемой в области . Непрерывн. ф-ии явл. интегрируемыми.
Геом. смысл . от ф-и >0 по области =объему цилиндра с основанием , ограниченного сверху поверхностью 
.
Св-ва:
если ф-и и 
интегрируемы в обл. , то интегрируемы в этой обл. их сумма и разность. Причем 
постоянный множитель можно выносить за знак интеграла
если интегрируема в обл. и обл. разбита на 2 непересек области 
и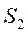 
, тогда двойной интеграл в области .
если ф-и 
и 
интегрируемы в обл. , причем £ 
, тогда 
если ф-я интегрируема в обл. , то ф-я 
также интегрируема в этой обл.. Причем 
если ф-я интегрируема в обл. , причем для 
из этой обл. выполн нер-во 
, тогда 
, где 
– площадь обл .
Вычисл двойного интеграла в прямоуг. Декартовых координатах.
При вычислении внутреннего интеграла 
считается постоянным. Правую часть ф-лы наз-ют повторным интегралом. 
= 
Ст-тной областью в данном направлении (направление данной оси) наз такая обл., для к-рой любая прямая параллельная этой оси и имеющая с дано обл. общие точки, пересекает границу не более 2 раз. В направлении оси Оу-область ст-тная, в направлении оси Ох-обл. ст-тной не явл.
Если обл. интегрирования не удовлетв. условиям ст-тной обл., каждая из к-рых была бы ст-тна в направлении одной из осей, необходимо разбить обл. интегрирования и вычислить двойные интегралы по каждой части отдельно.
Тройной интеграл.
Рассм. ограниченную замкнутую пространственную обл. 
и определенную в ней ф-ю 
. Аналогично строится интегральная сумма по данному объему и определяется тройной интеграл от ф-и 
по пространственной обл. 
Св-ва тройного интеграла (обладает св-вами двойного интеграла):
предположим, что обл. явл. ст-тной в направлении оси 
, т.е. удовлетворяет след. условиям:
(условие ст-тной обл.)
проекция обл. на плоскость 
представляет собой ст-тную обл. по оси Ох или Оу.
Если ст-тная обл. ограничена сверху поверхностью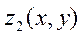 
, снизу - 
, а проекция обл. на плоскость 
определяется нер-вом 
т.е. обл. ст-тная, тогда 
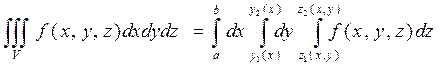
Замечание. Если проекция обл. на плоскость представляет собой ст-тную обл. по оси Ох и определяется нер-вом.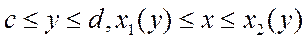 
, тогда
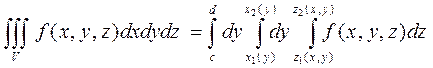
Замечание. Если обл. явл. ст-тной в напр-и каждой оси и ее проекции на коорд. пл-сти явл. ст-тными в направлении каждой соотв-щей оси, то пределы интегрирования в тройном интеграле можно расставить 6 различными способами.
Замечание. Если обл. представляет собой параллелепипед, ограниченный 
, тогда 
. Т.к. параллелепипед явл. ст-тной обл. в направлении любой из осей и его проекции также явл. ст-тными в направлении каждой из соотв. осей, то в данном интеграле пределы интегрирования можно расставить 6 способами.
Вопрос №34. Числовые и функциональные ряды.
Числовые ряды.
Числовой ряд -символ, обозначаемый 
Числа 
наз-ют членами этого ряда.
Суммы конечного числа членов этого ряда 
наз-ют частичными суммами или отрезками данного ряда.
Рассм. послед-сть 
. Если сущ-ет 
, то ряд наз-ют сходящимся, число –суммой этого ряда. Если послед-сть не имеет предела, то ряд расходящийся.
Св-ва числовых рядов:
если из членов ряда отбросить 
первых членов, то получим ряд 
, к-рый наз 
–ным остатком. Остаток данного ряда сходится и расходится одновременно с исходным рядом. Это означает, что при исследовании сходимости ряда можно отбрасывать конечное число первых членов.
(необходимый признак сходимости). Общий член сходящегося ряда ®0, т.е.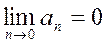 
, что не явл. достаточным признаком.
если ряд 
сходится и его сумма = , то ряд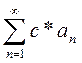 
также сходится, и его сумма = 
если 2 числ ряда 
и 
сходятся, тогда ряд 
Положительные ряды.
Полож. рядо м наз ряд, члены к-рого неотриц.
Признак сравнения.
Пусть даны 2 «+» ряда (1) и 
(2) начиная с нек-рого номера вып-тся условие 
, тогда из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).
Признак Даламбера.
Если члены «+» -ного ряда таковы, что сущ-ет предел 
, тогда если r<1 -ряд сходится; r>1 - расходится; r=1 -нужны доп. исследования.
