Этот метод основан на рав-ве 
.
Вопрос №10.Векторы и действия над ними.
Прямоуг. Декартова с-ма координат в пространстве.
Декартова с-ма корд. в пространстве определяется заданием масштабной единицы измерения длин и трех пересекающихся в одной точке 0 взаимноперпендик осей 
. О-начало координат. 
-ось абсцисс, 
-ось ординат, 
-аппликат.
Пусть М-произвольная точка пр-ва. Проведем через точку М 3 плоскости, ^ осям. Точки пересечения обозначим 
. Декартовыми коорд точки М в пр-ве наз числа 
, соотв. точкам 
.
Понятие вектора.
Любая упорядоченная пара точек А и В в пр-ве определяет направленный отрезок- вектор. А-начало вектора, В-конец вектора. Обозначают 
Модуль вектора - его длина и обозн 
. Нулевой вектор -вектор, начало и конец кот совпадают. Единичный вектор -вектор, длина кот равна 1.
Вектора 
и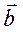 
наз коллинеарными если они лежат на параллельных прямых. Векторы 
и 
наз равными, если они коллинеарны и имеют равные длины.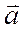 
и 
наз противоположными 
, если они коллинеарны, противоположны и имеют равные длины.
3 вектора 
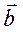, и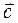 
наз компланарными, если они лежат в одной плоскости. Сумма 2х векторов и 
-вектор 
, начало кот совпадает с началом вектора 
, а конец – с концом 
.
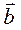Есл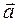и 
и 
имеют общее начало, то сумма совпадает с диагональю параллелограмма, построенного на этих векторах.
Св-ва суммы:
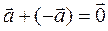
Разностью 2х векторов 
и наз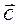 
, такой, что 
. Обозн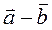 
Произведение вектора , отличного от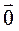 
, на число 
, наз вектор ,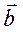 
, удовлетворяющ. след. условиям:
и 
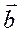коллинеарны
если a>0, то векторы одинаково направлены, если a<0-противоположно направлены.
Св-ва:
Два вектора коллинеарны тогда и только тогда, когда 
, для нек-рого действительного числа .
Проекция вектора на плоскость
Пусть в пр-ве задана нек-рая ось 
и нек-рый вектор АВ. Проекцией вектора АВ на ось 
наз величина вектора 
,взятая со знаком «+», если направление совпадает с направлением оси 
и со знаком «-«- если направлен противоположно. 
Св-ва:
Координаты вектора.
Пусть в пр-ве задана прямоуг. с-ма координат 
и произвольный вектор АВ.
Пусть 
Проекции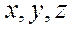 
вектора АВ наз-ют координатами 
Т. Для любых двух точек А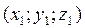 
и В 
координаты АВ определяются по ф-ле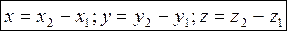 
Длина вектора.
Пусть произвольный вектор 
. Построим равный ему вектор, начало к-рого совпадает с началом координат. Проведем через конец вектора 
плоскости ^ осям координат. Вместе с координатными осями и координатными плоскостями образуют прямоугольный параллелепипед, диагональю к-рого служит отрезок ОА.
Вопрос №11.Скалярное, векторное и смешанное произведение векторов.
Разложение вектора по базисным векторам.
Пусть задана прямоуг. с-ма координат. Введем в рассмотрение единичные векторы,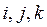 
коорд. осей 
. 
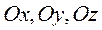-базисные вектора с-мы координат или орты. 
-произвольный вектор пр-ва. Отложим из начала координат вектор 
. По св-вам координат 
. Пусть числу 
на оси Ох соотв-ет точка 
, на 
. Тогда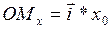 
, 
, 
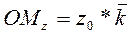
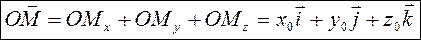- ф-ла разложения по базисным векторам.
Пр. (1;2;3)
(1;0;0)+2(0;1;0)+3(0;0;1)= 
