Деление отрезков в данном отношении.
Дано: произв отрезок М1М2 и пусть М-произв. т этого отрезка, отличная от М2. Число  - отношение, в к-ром М делит отрезок М1М2. Если
- отношение, в к-ром М делит отрезок М1М2. Если  делит отрезок М1М2 в отнош. l, то корд. этой точки определяются рав-вом
делит отрезок М1М2 в отнош. l, то корд. этой точки определяются рав-вом  , где
, где  -коорд. М1,
-коорд. М1,  -М2.
-М2.
Площадь треугольника.
Т. Для любых точек  не лежащих на одной прямой,
не лежащих на одной прямой,  выражается ф-лой
выражается ф-лой

Вопрос №4.Угол между прямыми на плоскости.
Рассм 2 прямые  ,
,  и
и 
 Углом между прямыми
Углом между прямыми  и
и  наз меньший из смежных углов, образованных этими пересекающимися прямыми. Очевидно, что jÎ[0;p]. Не сложно заметить, что
наз меньший из смежных углов, образованных этими пересекающимися прямыми. Очевидно, что jÎ[0;p]. Не сложно заметить, что  . Тогда
. Тогда 
 , то
, то  -это
-это  ,
,  -это
-это  Þ
Þ  . Если прямые параллельны, тогда Ðj=0,
. Если прямые параллельны, тогда Ðj=0, 
 . След-но
. След-но  =
=  - условие параллельности прямых. Если прямые ^, то
- условие параллельности прямых. Если прямые ^, то 
 ,
,  , след-но
, след-но  , т.е.
, т.е. 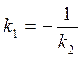 - условие перпендикулярности прямых.
- условие перпендикулярности прямых.
Вопрос №3.Ур-ние прямой на плоскости
Пусть на пл задана прямоуг. с-ма координат и нек-рая линия  .Ур вида
.Ур вида  связывающее переменные
связывающее переменные  и
и  наз ур линии
наз ур линии  (в заданной с-ме координат); если этому ур-нию удовлетвор коорд любой точки, лежащей на линии
(в заданной с-ме координат); если этому ур-нию удовлетвор коорд любой точки, лежащей на линии  и не удовлетворяют координаты никакой др точки, не лежащей на линии
и не удовлетворяют координаты никакой др точки, не лежащей на линии  .
.
Ур-ние прямой с угловым коэффициентом.
Пусть  прямая, не параллельная оси Оу.
прямая, не параллельная оси Оу.
Обозначим точки пересечения  с Оу точкой В, а угол между полож. направлением оси Ох и
с Оу точкой В, а угол между полож. направлением оси Ох и  обозначим j. Ðj наз углом наклона
обозначим j. Ðj наз углом наклона  к Ох (и в пределах от [0;p)). Пусть М(х,у)- произвольная точка прямой.
к Ох (и в пределах от [0;p)). Пусть М(х,у)- произвольная точка прямой. 
 Величину
Величину 
 обозначают
обозначают  и наз угловым коэффициентом прямой. Тогда ур примет вид
и наз угловым коэффициентом прямой. Тогда ур примет вид  –ур-е прямой с угловым коэфф, в частности если
–ур-е прямой с угловым коэфф, в частности если  =0, то j=0, прямая параллельна оси Ох. с ур-нием
=0, то j=0, прямая параллельна оси Ох. с ур-нием  если
если  =0 и
=0 и  получаем ур-ние оси Ох.
получаем ур-ние оси Ох.
Уравнение прямой по точке и  .
.
Пусть данная прямая имеет угловой коэф.  и проходит через точку
и проходит через точку  . Искомое ур-ние прямой
. Искомое ур-ние прямой  . Подставим коорд. точки М1в ур-ние
. Подставим коорд. точки М1в ур-ние 

Ур-ние прямой, проходящей через 2 данные точки.
Пусть искомая прямая прох через точки  и
и  . Искомое ур
. Искомое ур 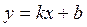 , где
, где  и
и  неизвестны. Т.к. прямая прох через М1, то
неизвестны. Т.к. прямая прох через М1, то  , т.к. прямая прох через М2, то
, т.к. прямая прох через М2, то  . Выразим из первого ур-ния
. Выразим из первого ур-ния  и подставим во второе
и подставим во второе 

Общее ур-ние прямой.
Т. Каждая прямая на плоскости с прямоуг. с-мой корд. определяется ур-нием первой степени  , где
, где  и
и  одновременно не равны 0.
одновременно не равны 0.  определяет нек-рую прямую на плоскости.
определяет нек-рую прямую на плоскости.
Это ур-ние называют общим ур-нием прямой на плоскости.
Ур-ние прямой, отрезка на осях координат.
Пусть прямая пересекает Ох и Оу соотв-но в точках А и В. Применяем ф-лу ур-ния прямой по двум точкам. Координаты А(а;0) и В(0;в): 
Получаем ур-ние  - ур-ние прямой на отрезках координат.
- ур-ние прямой на отрезках координат.
Вопрос №5. Расст от т до прямой на пл и взаим распол прямых на пл.
Расстояние от точки до прямой на плоскости.
Т. Расст.  от данной точки
от данной точки  до данной прямой
до данной прямой  , заданной ур
, заданной ур  на пл задается ф-лой
на пл задается ф-лой 
2)Взаимное расположение двух прямых на плоскости.
Пусть прямые  и
и  заданы своими общими ур-ми
заданы своими общими ур-ми 
Рассм. с-му, состоящих из этих ур-ний с неизвестными  и
и  .
.


1 случай:  ,
, 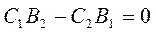 ур-ние имеет бескон множ-во решений. (прямые совпадают)
ур-ние имеет бескон множ-во решений. (прямые совпадают)  и
и 
2 случай:  ,
,  , т.е.
, т.е.  - ур-ние решений не имеет, т.к. прямые параллельны.
- ур-ние решений не имеет, т.к. прямые параллельны.
3 случай:  , ур-ние имеет единственное реш, т.е. прямые пересек в единственной точке.
, ур-ние имеет единственное реш, т.е. прямые пересек в единственной точке. 
Вопрос №6.Линии второго порядка на плоскости.
Линии, ур-ния к-рых в прямоуг. с-ме координат задаются ур-нием 2-ой степени наз линиями 2-го порядка. К важнейшим линиям второго порядка относят эллипс, окружность, гиперболу, параболу.
Окружность. Эллипс.
Эллипсом наз множ-во всех точек плоскости, для каждой из к-рых сумма расст до двух данных точек, наз-мых фокусом, есть величина постоянная, большее, чем расст между фокусами.
 Пусть
Пусть  имеет корд.
имеет корд.  ,
,  Запишем расстояние
Запишем расстояние  . Пусть постоянная величина, фигурирующая в определении эллипса = 2а
. Пусть постоянная величина, фигурирующая в определении эллипса = 2а 
 ;
;  >
> 
 >
> 

 (1)- каноническое ур-ние эллипса.
(1)- каноническое ур-ние эллипса.
Точки пересеч эллипса с осями коордт наз вершинами эллипса, оси симметрии(Ох и Оу) –осями эллипса. Осями также наз отрезки  . Отрезки
. Отрезки  и
и  наз-ют полуосями. В нашем случае А>В,
наз-ют полуосями. В нашем случае А>В,  -большая полуось,
-большая полуось,  -малая полуось. Эксцентриситетом наз отношения фокусного расст к длине большой оси и обозначают
-малая полуось. Эксцентриситетом наз отношения фокусного расст к длине большой оси и обозначают  . т.к.
. т.к.  >
>  >0, то 1>e>0. Фокальными радиусами точки М наз отрезки
>0, то 1>e>0. Фокальными радиусами точки М наз отрезки 
 и
и  , их длины равны.
, их длины равны.  . Ур (1) можно рассм и в случае когда
. Ур (1) можно рассм и в случае когда  >
>  . В этом случае большая полуось
. В этом случае большая полуось  равны
равны  . Фокусы такого эллипса лежат на оси Оу и
. Фокусы такого эллипса лежат на оси Оу и  . В случ, когда
. В случ, когда  =
=  получаем ур
получаем ур  , т.е. ур окр-ти.
, т.е. ур окр-ти.
Окружность - частный случай эллипса при равенстве полуосей. Для окружности  . Канон ур-ние окр имеет вид
. Канон ур-ние окр имеет вид  ,
,
Гипербола.
Гиперболой наз множ-во точек плоскости, для каждой из к-рых модуль разности расст до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расст. между фокусами.

 >
>  . Каноническое ур-ние гиперболы:
. Каноническое ур-ние гиперболы:  (2) Прямоугольник
(2) Прямоугольник  называется основным прямоугольником (рис.). Центр-начало координат. Прямые
называется основным прямоугольником (рис.). Центр-начало координат. Прямые  и
и  наз асимптотами гиперболы. Их ур-ние
наз асимптотами гиперболы. Их ур-ние  и
и  .Гипербола имеет 2 ветви. Центр симметрии наз центром гиперболы; оси симметрии наз осями гиперболы. Ось, к—рую пересек гипербола наз действительной осью, а ось непересек наз мнимой осью. Величины
.Гипербола имеет 2 ветви. Центр симметрии наз центром гиперболы; оси симметрии наз осями гиперболы. Ось, к—рую пересек гипербола наз действительной осью, а ось непересек наз мнимой осью. Величины  и
и  наз полуосями. Если
наз полуосями. Если  =
=  , то гипербола равносторонняя, её ур
, то гипербола равносторонняя, её ур  . Ур
. Ур  (3)определяет гиперболу с действительной осью Оу. Ур (2) и (3) в одной и той же с-ме координат наз сопряженными. Эксцентриситет гиперболы-это отношение фокусного расст к расст между вершинами, т.е. точками пересечения с осями координат. Для ур (2)
(3)определяет гиперболу с действительной осью Оу. Ур (2) и (3) в одной и той же с-ме координат наз сопряженными. Эксцентриситет гиперболы-это отношение фокусного расст к расст между вершинами, т.е. точками пересечения с осями координат. Для ур (2) 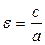 , т.к.
, т.к.  >
>  , то e>1.
, то e>1.
Парабола.
 Параболой наз множ-во точек плоскости, для каждой из к-рых расст от данной точки, наз фокусом равно расст до данной прямой, наз директрисой и не проходящей через фокус (рис.)
Параболой наз множ-во точек плоскости, для каждой из к-рых расст от данной точки, наз фокусом равно расст до данной прямой, наз директрисой и не проходящей через фокус (рис.)  - каноническое ур параболы.
- каноническое ур параболы. 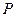 -наз параметом параболы, точку О-вершиной параболы, ось симметрии-осью параболы.
-наз параметом параболы, точку О-вершиной параболы, ось симметрии-осью параболы.
Вопрос №7. Матрицы и действия над ними.
Таблица чисел вида 
 , сост из
, сост из  строк и
строк и  столбцов наз матрицей размерности
столбцов наз матрицей размерности  ´
´  .
.
Числа  наз её элементами, если
наз её элементами, если  ¹
¹  , то матрицу наз-ют прямоугольной, если
, то матрицу наз-ют прямоугольной, если  =
=  , то квадратной. Если
, то квадратной. Если  =1, а
=1, а  >1, то матрица примет вид
>1, то матрица примет вид  и наз матрицей-строкой. Если же
и наз матрицей-строкой. Если же  >1, а
>1, а  =1, то матрица наз матрицей-столбцом. Число строк в квадратной матрице наз ее порядком. Две матрицы наз равными если они имеют одинак. размерность и соответствующие элементы равны.
=1, то матрица наз матрицей-столбцом. Число строк в квадратной матрице наз ее порядком. Две матрицы наз равными если они имеют одинак. размерность и соответствующие элементы равны.
Сложение и вычитание матриц.
Суммой двух матриц А и В одинакового размера  ´
´  наз матрица С размерности
наз матрица С размерности  ´
´  , элементы кот равны сумме соотв эл-в матриц А и В.
, элементы кот равны сумме соотв эл-в матриц А и В.
Матрица 0 размерности  ´
´ 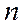 , все элементы к-рой=0 наз нулевой матрицей.
, все элементы к-рой=0 наз нулевой матрицей.
Разностью двух матриц А и В размерности  ´
´  наз матрица С размерности
наз матрица С размерности  ´
´  такая, что А=В+С. Из определения следует, что элементы матрицы С равны разности соотв. элементов матриц А и В.
такая, что А=В+С. Из определения следует, что элементы матрицы С равны разности соотв. элементов матриц А и В.
Св-ва сложения:
сложение матриц коммутативно, т.е. А+В=В+А
сложение матриц ассоциативно, т.е. (А+В)+С=А+(В+С)
А+0=0+А=А






