М-д непосредственного интегрирования.
Пример: 
М-д замены переменной.
Теорема: если F(x)-первообр. f(x),  -дифференц. ф-я. Тогда
-дифференц. ф-я. Тогда  также имеет первообр. Причем
также имеет первообр. Причем

Док-во: По правилам диф. сложной ф-и  дает
дает  , т.е.
, т.е.  -одна из первообр. для
-одна из первообр. для  . След-но
. След-но  .
.
Поскольку  совпадает с
совпадает с  , тогда
, тогда 
Пример: 
М-д интегрирования по частям основан на след. форме:



Интегрирование простейших рациональных дробей.

Интегрирование тригонометрических ф-ий.
Вычисл интеграла вида  ,
,  ,
,  ,
, 
 сводится к вычислению интегралов от рац. ф-ий, роль переменной играет t. если R(sin x cos x) явл. нечетной относительно sin x, то вводят замену cos x= t. Если R(sin x cos x) явл. нечетной относ-но cos x, то вводят замену sin x= t. Если ф-я R (sin x cos x)явл. нечетной относ-но sin x и cos x, то вводят замену tg x=t.
сводится к вычислению интегралов от рац. ф-ий, роль переменной играет t. если R(sin x cos x) явл. нечетной относительно sin x, то вводят замену cos x= t. Если R(sin x cos x) явл. нечетной относ-но cos x, то вводят замену sin x= t. Если ф-я R (sin x cos x)явл. нечетной относ-но sin x и cos x, то вводят замену tg x=t.



Интегрирование иррац. ф-и
Интегралы типа


 вычисляются путем полного квадрата под радикалом и дальнейшей заменой
вычисляются путем полного квадрата под радикалом и дальнейшей заменой 
Тригонометрическая подстановка
Интегралы вида






с помощью замен сводятся к интегралам от рац. ф-ий.
Вопрос №31. Определенные интегралы.
Опред. интеграл и его приложения.
О. Определенным интегралом от ф-и  на
на  наз конечный предел её интегральной суммы, когда число элемент. отрезков неограниченно возрастает, а длина наиб. из них стремится к нулю. Обозначается:
наз конечный предел её интегральной суммы, когда число элемент. отрезков неограниченно возрастает, а длина наиб. из них стремится к нулю. Обозначается: 
Число a наз нижним пределом интегрирования, b - верхним пределом интегрирования, f(x)- подинтегр ф-ей, х-переменной интегрирования.
По определению
 (1)
(1)
след-но велич опред интегр не зависит от переменной интегрир, т.е.

Ф-я, для к-рой существует предел (1) наз интегрированием на  .
.
Геом. смысл определенного интеграла состоит в том, что  =S криволин. трапеции, ограниченной сверху графиком ф-и
=S криволин. трапеции, ограниченной сверху графиком ф-и  (f(x)≥0), снизу осью Ох, слева и справа- прямыми х=а и х=в.
(f(x)≥0), снизу осью Ох, слева и справа- прямыми х=а и х=в.
Св-ва опред. интеграла:
 при перестановке пределов интегрирования, знак определенного интеграла меняется на противоположный
при перестановке пределов интегрирования, знак определенного интеграла меняется на противоположный

 если
если  и
и  интегрируемы на
интегрируемы на  ф-и, тогда
ф-и, тогда  ±
±  также интегрируемы. Причем
также интегрируемы. Причем
 св-во аддитивности. Пусть
св-во аддитивности. Пусть  разбит на
разбит на  элементарных отрезков след. образом
элементарных отрезков след. образом  , тогда
, тогда  постоянный множитель можно выносить за знак определенного интеграла.
постоянный множитель можно выносить за знак определенного интеграла.
если  интегрируема на
интегрируема на  (a<b), причем f(x)≥0, тогда
(a<b), причем f(x)≥0, тогда 
пусть ф-и f(x) и g(x) интегрируемы на  (a<b) и на всем отрезке f(x) ≤ g(x). Тогда
(a<b) и на всем отрезке f(x) ≤ g(x). Тогда 
пусть ф-я f(x) интегрируема на  (a<b), тогда
(a<b), тогда  также интегрируема на
также интегрируема на  , причем
, причем 
Теорема. (об оценке опред. интеграла). Если ф-я  интегрируема на
интегрируема на  (a<b) и для всех
(a<b) и для всех  вып-тся нерав-во
вып-тся нерав-во  , тогда
, тогда

Теорема. (о среднем значении) Если ф-я  непрерывна на
непрерывна на  , то на этом отрезке существует точка с, такая что
, то на этом отрезке существует точка с, такая что 
Опред. интеграл с переменным верхним пределом(ОИПВП).
Рассм. ф-ю  , интегрируемую на
, интегрируемую на  . Пусть
. Пусть  , тогда
, тогда  интегрируема на любом отрезке
интегрируема на любом отрезке  .Предпол, что х меняется на этом отрезке, тогда определена ф-я Ф(х)=
.Предпол, что х меняется на этом отрезке, тогда определена ф-я Ф(х)=  . Данную ф-ю наз ОИПВП. ОИПВП явл. непрерывной на
. Данную ф-ю наз ОИПВП. ОИПВП явл. непрерывной на  ф-ейесли
ф-ейесли  явл. непрерывной, то производная с ОИПВП= значению подинтегральной ф-и для данного предела интегрирования, т.е.
явл. непрерывной, то производная с ОИПВП= значению подинтегральной ф-и для данного предела интегрирования, т.е. 
ОИПВП явл. одной из первообр. для непр. подинтегральной ф-и.
Теор.(ф-ла Ньютона-Лейбница). Пусть ф-я  непрер на
непрер на  , тогда если ф-я F(x) явл. некот её первообр. на
, тогда если ф-я F(x) явл. некот её первообр. на 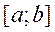 , то справедлива след. ф-ла
, то справедлива след. ф-ла

Основные методы интегрирования:
Т. (о замене переменной в определенном интеграле). Пусть  -непрерывна на
-непрерывна на  ф-я, тогда если: 1)ф.
ф-я, тогда если: 1)ф.  дифференцируема на
дифференцируема на  и
и  –непрерывна на
–непрерывна на  . 2)множ-вом значений ф-и
. 2)множ-вом значений ф-и  явл.
явл.  . 3)
. 3)  ,
,  . тогда справедлива ф-ла:
. тогда справедлива ф-ла:

По ф-ле Ньютона-Лейбница, где  - нек-рая первообразная
- нек-рая первообразная  на
на  .
.
Т. (об интегрировании по частям) Если ф-и  и
и  непрерывны вместе со своими производными
непрерывны вместе со своими производными  и
и 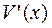 на
на  , то справедлива след. ф-ла:
, то справедлива след. ф-ла:

Приложение определенного интеграла.






