Конечная с-ма векторов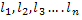 
простр-ва V наз линейно зависимой, если найдутся такие числа 
, из кот-х хотя бы одно ≠0, такие что 
(совп с нейтральным эл-том).
В противном случае с-му наз линейно независимой.
Лемма. Система векторов простр-ва V явл-ся линейно зависимой, если один из векторов линейно выражается через остальные.
Выр-е вида 
наз линейной комбинацией векторов 
Сис-ма векторов 
наз базисом пространства V, если:
1) с-ма векторов 
линейно независима
2)любой вектор пр-ва V линейно выр-ся через
Число n называется размерностью простр-ва V, если в этом пространстве сущ-ет n линейно независимых векторов, а любые n+1 векторы линейно зависимы.
Т. В простр-ве V разм-ти n любая с-ма, состоящая из n линейно независимых векторов, образует базис.
Если - базис простр-ва V, то 
называют разложением вектора x по векторам базиса. В этом случае наз координатами вектора x в базисе
Вопрос №17. Функция. Предел ф-и.
Ф-я. Рассм. множ-во 
элементов 
и множ-во 
элементов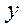 
. Если каждому элементу 
из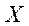 
поставлен в соотв-е единственный элемент 
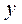из 
обозначаем 
, то говорят: на множ-ве 
задана ф-я 
со значениями в множ-ве 
. Элементы 
значение аргумента; 
-значение ф-и; множ-во 
–область определения; множ-во всех значений ф-и – областью значений ф-и.
К основным способам задания ф-и относят:
1. Аналитический. Ф-я, заданная ф-лой 
, правая часть к-рой не содержит 
наз явной ф-ей. Ф-я 
наз заданной не явно.
2. Табличный способ- способ задания ф-ии при помощи таблицы (Н.:логарифмич. таблицы, тригонометрические и т.д.)
3. Графический-при помощи графика. Графиком ф-и 
наз множ-во точек плоскости с координатами 
плоскости 
, где 
.
сложная ф-я или композиция.
Степенные, показательные, логарифмические, тригонометрические, обратные тригонометрические наз основными элементарными ф-ями. Элементарными наз ф-ии, к-рые можно получить из основных элементарных с помощью алгебраических действий и композиций.
Предел ф-и.
О. Число А наз пределом ф-и 
, при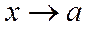 
(или в точке 
). Если для любого числа 
>0, сущ-ет такое число d>0, что при всех 
, удовлетворяющих условию 0< 
<d вып-тся нер-во 
<e.
Для 
0< 
<d (1) Þ 
<e.
Обозначается 
Геометрический смысл определения. Нер-во (1) означает, что расположено от 
на расстоянии не более d, т.е. 
за исключением самой точки 
. Нер-во (2) означает, что значение ф-и 
не выходит из интервала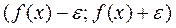 
или 
. След-но точки графика ф-и должны находится в полосе шириной 2e, если 
Односторонние пределы.
О. Число А наз правым(левым) пределом ф-и 
в точке 
, если для "e>0 сущ-ет d>0, такое,что для всех 
, удовлетворяющих рав-ву 
< 
< +d ( -d< < ); <e.
"e>0 $d>0: " 
< < +d ( -d< 
< )Þ 
<e.
Связь между односторонними пределами.
Ф-я 
имеет в 
предел только тогда, когда в этой точке сущ-ет как левый так и правый предел и они равны. В этом случае предел ф-и равен одностороннему пределу.
Пределы ф-и при стремлении аргумента к бесконечности.
О. Пределом ф-и 
при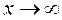 
наз число А такое, что для "e>0 $d>0: " 
>dÞ 
<e. Обозначают 
.
О. Число наз пределом ф-и при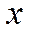 
®+¥ ( ®-¥) если для "e>0 $d>0: " 
>d( <-d)Þ 
(
).
