Линейное ОДУII с постоянными коэффициентами имеет вид:
(1), где 
, а f(x) – некоторая функция.
Если f(x) = 0, то уравнение 
(2) называется однородным.
В противном случае (т.е. уравнение (1)) – неоднородным.
Можно доказать, что существует единственное решение уравнения (1), удовлетворяющее начальным условиям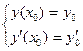 
.
Рассмотрим сначала решение однородного уравнения (2).
Метод решения этого уравнения состоит в следующем: по виду уравнения (2) составляется характеристическое уравнение 
(3).
Описание решений уравнения (2) зависит от того, имеет ли уравнение (3) два действительных корня, один действительный корень или не имеет действительных корней.
Теорема:
1) Пусть характеристическое уравнение (3) имеет два различных действительных корня k1 и k2 (т.е. D>0). Тогда общее решение уравнения (2) имеет вид:
.
2) Если уравнение (3) имеет один действительный корень k (кратности 2) (D=0), то общее решение уравнения (2): 
.
3) Если уравнение (3) не имеет действительных корней (D<0), то общее решение уравнения (2): 
,
где 
, 
.
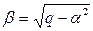4. Решить краевую задачу для уравнения второго порядка
, 
, 
.
Решение. Решив данную задачу мы получим частное решение линейного ОДУII с постоянными коэффициентами при указанных начальных условиях.
Чтобы найти частное решение дифференциального уравнения, необходимо сначала найти его общее решение.
Составим и решим соответствующее характеристическое уравнение 
.
Данное характеристическое уравнение имеет 1 действительный корень k = 1. Поэтому общее решение уравнения имеет вид: у = С 1 ех + С 2 хех (формула (3.5)).
Теперь найдем такие значения постоянных С 1 и С 2, при которых выполняются заданные начальные условия. Т.к. у (0) = С 1, а у (1) = С 1 е + С 2 е, то постоянные находим, решая систему
.
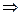
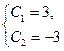Т.о. частное решение уравнения у = 3 ех – 3 хех.
Ответ: Решение данной краевой задачи имеет вид: у = 3 ех – 3 хех.
Перейдем к решению линейного неоднородного уравнения (1).
Рассмотрим два метода решения этого уравнения:
1) метод вариации произвольных постоянных.
Сначала находим общее решение 
соответствующего однородного уравнения (2). Затем решение уравнения (1) ищут в виде 
, т.е. С1, С2 – функции независимой переменной х. Их находят из системы: 
2) метод подбора частного решения:
Теорема: Общее решение линейного неоднородного уравнения (1) равно сумме общего решения соответствующего однородного уравнения (2) у* и некоторого частного решения уравнения (1) 
: 
.
Одним из способов нахождения является подбор по виду правой части f(x). Приведем в виде таблицы наиболее часто встречающиеся виды правых частей и соответствующие им виды частных решений.
| № | Вид правой части f(x) | Корни уравнения (3) | Вид
|
| a | 0 – не корень 0 – корень | A Ax | |
| aх + b | 0 – не корень 0 – корень | Ax + B x(Ax + B) | |
| aх2 + bx + c | 0 – не корень 0 – корень | Aх2 + Bx + C x(Aх2 + Bx + C) | |
| aemx | m – не корень m–однократный корень m–двукратный корень | Aemx Axemx Ax2emx | |
| (aх + b)emx | m – не корень m–однократный корень m–двукратный корень | (Ах + В)emx х(Ах + В)emx х2(Ах + В)emx | |
| a∙ cos nx + b∙ sin nx |  in – не корни
in – корни
| A∙ cos mx + B∙ sin mx x(A∙ cos nx + B∙ sin \nx) |
В таблице А, В, С – неизвестные коэффициенты, которые находят путем подстановки частного решения в исходное дифференциальное уравнение (1) и приравнивания коэффициентов при одинаковых функциях в левой и правой частях полученного равенства.
Если правая часть f(x) имеет вид суммы или произведения функций типов 1-6, то частное решение также следует подбирать в виде соответствующей суммы или произведения.
Пример. 
.
Это уравнение является линейным неоднородным ОДУII с постоянными коэффициентами.
Чтобы его решить нужно:
1) Найти общее решение соответствующего однородного уравнения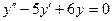 
.
Для этого составим характеристическое уравнение и найдем его корни: 
, k 1 = 2, k 2 = 3. Т.к. мы получили 2 различных действительных корня (это случай 1), то по формуле (3.4) общее решение однородного уравнения имеет вид у* = С 1 е 2 х + С 2 е 3 х .
2) Подобрать частное решение неоднородного уравнения.
Правая часть f(x)= ех. Это случай 4 из таблицы 2. И поскольку m = 1 не является корнем характеристического уравнения, то частное решение должно иметь вид = Aex (1-ая строка пункта 4 таблицы 2). Найдем первую и вторую производные частного решения: ’= Aex; ”= Aex. Подставляя , ’, ” в исходное уравнение, получаем:
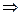
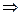
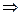
. Т.о. частное решение уравнения = 
ex.
Т.к. , то общее решение имеет вид у = С 1 е 2 х + С 2 е 3 х + ex.
Ответ: Общее решение уравнения имеет вид
у = С 1 е 2 х + С 2 е 3 х + ex.
