Опр.: ОДУI называется уравнением с разделяющимися переменными, если его можно привести к виду: f1(x)dx = f2(y)dy.
Такими уравнениями являются:
а) 
;
б) Р1(х)Р2(у)dx + Q1(x)Q2(y)dy = 0.
Пример 1. а) Найти общее решение уравнения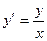 
(х ¹0).
Решение: Данное уравнение относится к ОДУI с разделяющимися переменными (вид а). Приведем уравнение его к виду f1(x)dx = f2(y)dy.
Поскольку 
, то получаем 
.
Умножим полученное уравнение на dx и разделим на у: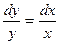 
.
Затем проинтегрируем обе части уравнения: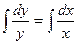 
=> 
. Используя свойства логарифмов, имеем: 
, откуда получаем решение
у = Сх (х ≠0).
Ответ: Общим решением уравнения 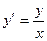является функция у = Сх (х ≠0).
б) Найти общее решение уравнения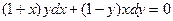 
.
Решение: Это уравнение также является ОДУI с разделяющимися переменными (вид б). Поэтому разделим переменные, перенеся второе слагаемое в правую часть уравнения и разделив затем обе части уравнения на х и у:
; 
.
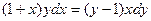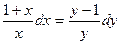Интегрируем обе части уравнения: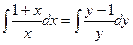 
.
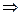
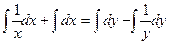
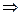
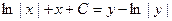
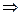
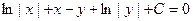
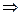
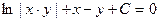Общее решение получили в виде общего интеграла.
Ответ: общее решение уравнения .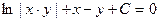
в) Найти решение задачи Коши: 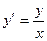, у (1) = 2 (х ¹0).
(Или, другими словами, найти частное решение данного уравнения при заданном начальном условии).
Решение: Частные решения получаются из общего при конкретных значениях произвольной постоянной С. Поэтому сначала находим общее решение уравнения: у = Сх (См. пример 1а).
А затем, используя начальное условие, получим: 2 = С ×1 => С = 2.
Т.о. окончательно имеем: у = 2 х.
Ответ: решение задачи Коши у = 2 х.
Однородные ОДУI
Опр.: ОДУI y’ = f(x, y) называется однородным, если для функции f(х, у) выполняется равенство: f(kx, ky) = f(x, y), где k – постоянная.
Однородное уравнение м.б. записано в виде: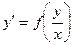 
. Поэтому заменой 
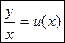оно сводится к дифференциальному уравнению с разделяющимися переменными. (Отметим, что если у = x∙u, то y’ = u + xu’ = u + x∙ 
.)
Пример 2. Найти общее решение уравнения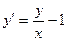 
.
Решение. Данное ОДУ1 является однородным, т.к. f(kx, ky) = 
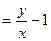= f(x, y).
Поэтому заменим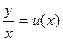 
, y’ = u + x∙ . Тогда относительно новой функции получим уравнение с разделяющимися переменными:
u + x∙ = u – 1.
Разделяя переменные и интегрируя, получим:
x∙ = – 1 => du =∙– 
=> u =∙ ln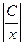 
.
Заменив ∙u =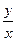 
, окончательно получаем общее решение: у =х∙ ln .
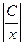Ответ: Общее решение уравнения у =х∙ ln .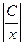
Линейные ОДУI
Опр.: Линейным ОДУI называется уравнение, линейное относительно неизвестной функции и ее производной:
у’ + p(x)y = q(x) (1),
где p(x), q(x) - заданные непрерывные функции от х или константы.
Решение следует искать в виде у = u∙v (2),
где u(x) – ненулевое частное решение уравнения с разделяющимися переменными
u’ + p(x) ∙u = 0 (3), а v(х) – новая неизвестная функция.
Подставляя (2) в (1) имеем:
u’∙v + v’∙u + p(x) ∙u∙v = q(x) Þ (u’ + p(x) ∙u)∙v + v’∙u = q(x), учитывая (3), находим, что новая неизвестная функция v(x) будет удовлетворять уравнению:
v’∙u = q(x) (4 ).
Уравнения (3) и (4) являются уравнениями с разделяющимися переменными, из них находим u(x), v(x), причем для u(x) выбирается частное решение ≠ 0.
Затем найденные функции подставляем в (2).
Пример 3. Найти общее решение уравнения 
.
Решение. Это линейное ОДУ1, где p(x) = 
, q(x) = х.
Решение ищем в виде у = uv. Для того, чтобы найти функцию u, решаем уравнение вида (3) с разделяющимися переменными: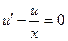 
.
=> 
=> 
=> 
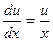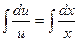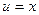
(при интегрировании считаем, что произвольная постоянная С = 0).
Затем подставляем u в уравнение вида (4) и получаем также уравнение с разделяющимися переменными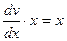 
.
Решаем: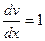 
=> dv = dx => 
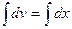=> v = x + C.
Т.о. имеем у = uv = х(х + С).
Ответ: Общее решение уравнения у = х(х + С).
В.3. ОДУII
ОДУII в общем виде: F(x, y, y’,y’’) = 0.
Если оно разрешено относительно у’’, то имеет вид: y’’ = f(x, y, y’).
Опр.: Задача нахождения решения уравнения y’’ = f(x, y, y’), удовлетворяющего начальным условиям: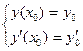 
(где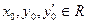 
), называется задачей Коши.
Опр.:Общим решением ОДУII называется функция у = φ(х, С1, С2), зависящая от двух произвольных постоянных С1, С2 при следующих условиях:
1) она является решение уравнения при любых значениях С1, С2;
2) при любых начальных условиях 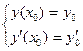существуют единственные значения С1 = С1 0, С2 = С2 0 такие, что у = φ(х, С1 0, С2 0) удовлетворяет данным начальным условиям.
Начальные условия можно задать и по-другому.
Пусть, например, решение ищется на отрезке [a, b]. Тогда для определения С1 0, С2 0 можно задать условия: 
, т.е. задачу для ОДУII можно сформулировать следующим образом: на отрезке [a, b] найти решение ОДУII, удовлетворяющее условиям, заданным на концах отрезка.
F(x, y, y’,y’’) = 0, . Такая задача называется краевой задачей для ОДУII.
