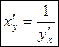Пусть функция y = ƒ(x) определена на множестве Х. Возьмём т. х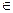 
Х. Дадим значению х приращение 
. Тогда y подучит приращение 
.
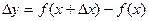Определение. Производной функции y = ƒ(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
.
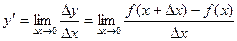Другие обозначения: 
Дифференцирование функции – это нахождение производной этой функции. Если функция имеет в точке x производную (конечную), то она называется дифференцируемой в этой точке. То же можно сказать о дифференцировании функции на промежутке X.
Геометрический смысл производной: производная – угловой коэффициент или тангенс угла наклона касательной, проведенной к кривой y= f(x) в точке x0, с осью Ох.
Уравнение касательной к кривой y= f(x) в точке x0: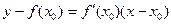 
.
Механический смысл: производная пути по времени 
- есть скорость точки в момент t0, т.е.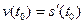 
.
Теорема (зависимость между непрерывностью и дифференцируемостью): Если функция y= f(x) дифференцируема в точке x0, то она в этой точке непрерывна.
Обратная теорема, вообще говоря, не верна, т.е. непрерывная функция может быть не дифференцируемой в точке x0, например, функция y =|x| в точке x=0.
Поэтому непрерывность функции является необходимым, но не достаточным условием дифференцируемости функции. В математике известны непрерывные функции, не дифференцируемые ни в одной точке.
Замечание. Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на промежутке X, то функция называется гладкой на этом промежутке. Если производная допускает конечное число точек разрыва 1-го рода, то она называется кусочно-гладкой на данном промежутке.
В.3. Основные правила дифференцирования
1) с’ = 0;
2) x’ = 1;
3) (u + v)’ = u’ + v’;
4) (c ∙ u)’ = c∙u’;
5) (u∙v)’ = u’ ∙ v + u ∙ v’;
6) (u∙v∙w)’ = u’∙v∙w + u∙v’∙w + u∙v∙w’;
7) 
.
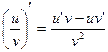В.4. Производная сложной и обратной функций
Если у есть функция от и: у = f(u), где и в свою очередь есть функция от аргумента х: u = φ(x), т.е. если у зависит от х через промежуточный аргумент и, то у называется сложной функцией от х (функцией от функции): y = f(φ(x)).
Теорема. Производная сложной функции 
, где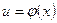 
, где y и u – дифференцируемые функции своих аргументов, равна произведению ее производной по промежуточному аргументу на производную этого аргумента по независимой переменной:
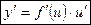или y’x = y’u u’x
.
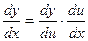Пусть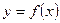 
–дифференцируемая и строго монотонная функция на промежутке X, 
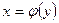– обратная к ней и непрерывная на соответствующем промежутке Y.
Теорема. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции, т.е. 
