Для дифференцируемой функции y = f(x)  . Если дифференциал независимой переменной
. Если дифференциал независимой переменной 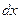 имеет произвольное, но фиксированное значение, не зависящее от х, то
имеет произвольное, но фиксированное значение, не зависящее от х, то  - некоторая функция от х, которая также может иметь дифференциал.
- некоторая функция от х, которая также может иметь дифференциал.
Дифференциалом n – го порядка (n – ым дифференциалом) называется дифференциал от дифференциала (n–1)–го порядка данной функции:

Дифференциал n – го порядка равен произведению производной n – го порядка на n – ю степень дифференциала независимой переменной.
 . (где
. (где  )
)
=>  . В отличие от дифференциала первого порядка дифференциалы более высоких порядков не обладают свойством инвариантности формы.
. В отличие от дифференциала первого порядка дифференциалы более высоких порядков не обладают свойством инвариантности формы.
Тема 3. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ (НИ)
1. Первообразная и неопределённый интеграл
Определение1: Функция F(x) называется первообразной для функции f(x) на промежутке Х, если в любой точке х Î Х: (F(x))’ = f(x).
Например, F(x)=  - первообразная для функции f(x)=х4.
- первообразная для функции f(x)=х4.
(Т.к. (F(x))’ =  f(x).)
f(x).)
Геометрический смысл: Найти первообразную для функции f(x) означает найти такую кривую у = F(x), что угловой коэффициент касательной к ней в произвольной точке х равен значению f(x) в этой точке. (((F(x))’= tga = f(x)).


Первообразная функции определена неоднозначно: если F(x) – первообразная для функции f(x), то F(x)+C – также первообразная для данной функции.
Теорема. Если F1(x) и F2(x) – первообразные для функции f(x) на промежутке Х, то существует такое число СÎ R, что F2(x) = F1(x) + С.
(Т.е все первообразные одной и той же функции отличаются друг от друга лишь на некоторую постоянную.)
Определение 2. Множество всех первообразных для функции f(x) называется неопределенным интегралом и обозначается 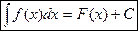 ,
,
где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, С – произвольная постоянная (С = const),  - знак операции интегрирования, d – знак операции дифференцирования.
- знак операции интегрирования, d – знак операции дифференцирования.
Теорема существования НИ. Любая непрерывная на некотором промежутке Х функция f(x) имеет первообразную на этом промежутке.
2. Основные свойства НИ:
1. Производная от НИ равна подынтегральной функции, а дифференциал – подынтегральному выражению:
 ,
, 
2. НИ от дифференциала некоторой функции равен этой же функции с точностью до некоторой постоянной:  .
.
В частности,  .
.
Замечание: Объединяя свойства 1 и 2, можно сделать вывод о том, что операции интегрирования и дифференцирования функции – это взаимообратные операции.
3. НИ от алгебраической суммы конечного числа функций равен такой же сумме интегралов НИ от этих функций

 .
.
4. Константу можно выносить за знак НИ:

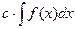 , где с = const.
, где с = const.
5. Свойство инвариантности формы НИ (т.е. независимости вида НИ от выбора аргумента):

В частности, 
Таблица НИ
Используя определение НИ и таблицу производных можно записать таблицу НИ.
Таблица 1 (неопределенных интегралов)
1.  2.
2.  3.
3.  n ≠ –1;
4. n ≠ –1;
4. 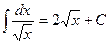 ;
5. ;
5.  ;
6. ;
6.  ;
7. ;
7.  ;
8. ;
8.  ; ;
| 9.  ;
10. ;
10.  11.
11.  ;
12. ;
12.  (| x |< a, a ≠0);
13. (| x |< a, a ≠0);
13.  (a ≠0);
14. (a ≠0);
14.  (| x |≠ a, a ≠0);
15. (| x |≠ a, a ≠0);
15.  . .
|
Методы интегрирования
Метод разложения
Метод разложения заключается в разложении подынтегральной функции на сумму функций и использовании свойств неопределенного интеграла 3 и 4. Применяется, если интегралы от слагаемых табличные или известен метод их вычисления.
Пример 1. 
 =
=  =
=  =(св-во 3) =
=(св-во 3) =
=  = (св-во 4) =
= (св-во 4) =  = (используем формулы 3 и 4 из таблицы 1 н.и.)=
= (используем формулы 3 и 4 из таблицы 1 н.и.)= 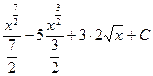 =
=
=  .
.
Ответ:  =
=  .
.
Метод замены переменной
Формула замены переменной: 
 ,
,
где х = j(t) – дифференцируемая функция на промежутке Х.
Пример 2.  .
.
Данный интеграл вычисляется методом замены переменной (линейная замена). Обозначим выражение в скобках через t: 3 х – 1 = t, тогда d (3 х – 1)= dt => 3 dх = dt =>  .
.
 =
=  =
= 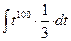 =
=  = (по формуле 3 из таблицы 1 н.и.) = =
= (по формуле 3 из таблицы 1 н.и.) = =  =
=  =
= 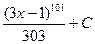 .
.
Ответ:  =
= 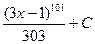 .
.
Пример 3.  .
.
Здесь при вычислении интеграла используется также метод замены переменной (нелинейная замена).
 =
=  =
=  =
= 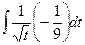 =
=  = (используем формулу 4 из табл.1 н.и.) =
= (используем формулу 4 из табл.1 н.и.) =  =
=  .
.
Ответ:  =
=  .
.






