С учётом полученного правила дифференцирования сложной функции таблицу производных можно записать в следующем виде:
Таблица производных
| № | Функция у | Производная у’ |
| С | ||
| x | ||
| un | n∙un-1∙ u’ | |
| 
| |
| 
| |
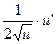
| eu | eu∙u’ | |
| au | au ∙ln a ∙ u’ | |
| ln u | 
| |
| loga u | 
| |
| sin u | cos u∙u’ | |
| cos u | – sin u∙u’ | |
| tg u | 
| |
| ctg u | 
| |
| arcsin u | 
| |
| arcos u | –
| |
| arctg u | 
| |
| arcctg u | –
|
Пример 1. Найти производную функции:
а) у = х + 2; б) y = (2 x – 3)(3 x + 2); в) у = 
; г) у = 
; д) у = (x 3 – 2 x 2 + 5)6; е) 
; ж) 
; з) y = tg(3 x 2 – 1); и) 
.
Решение. а) у = х + 2
Используя правило дифференцирования (3) и формулы (1), (2), имеем:
у' = (x + 2) ’ = (x) ’ + (2) ’ = 1 + 0 = 1.
б). y = (2 x – 3)(3 x + 2)
y’ = ((2 x – 3)(3 x + 2)) ’ = (2 x – 3) ’ ∙(3 x + 2) + (2 x – 3)∙(3 x + 2) ’ = 2∙(3 x + 2) + (2 x – 3)∙3 = 12 x – 5. Здесь мы использовали правило дифференцирования (5).
в) у =
Используя правило дифференцирования (7), имеем
у’ = 
= 
.
г) у =
Найдем производную, используя правило дифференцирования (4) и формулу (3).
у' =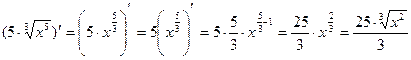 
.
д) у = (x 3 – 2 x 2 + 5)6
Пусть x 3 – 2 x 2 + 5 = и, тогда у = и 6. По формуле (3), получим у’ = (и 6) ’ = 6 u 5∙ u’ = 6(x 3 – 2 x 2 + 5)5∙(x 3 – 2 x 2 + 5) ’ = 6(x 3 – 2 x 2 + 5)5∙(3 x 2 – 4 x).
е)
По правилу дифференцирования (7) и формуле (10) получим:
= 
.
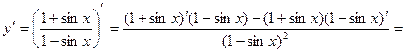
ж)
Используя формулы (4) и (10), имеем:
.
з) y = tg(3 x 2 – 1).
По формуле (12) имеем:
y' = (tg(3 x 2 – 1)) ’ = 
.
и) .
По формуле (8), а также (3), (4), (5) имеем:
=
= 
.
В. 6. Производная степенно-показательной функции
Производная степенно-показательной функции 
:
Т.е. для того чтобы найти производную степенно-показательной функции, нужно сначала продифференцировать её как степенную (формула (3)), затем как показательную (формула (7)) и полученные результаты сложить.
Пример 2. Вычислить производную функции 
.
Решение. 
.
Производная неявной функции F(x,y)=0 получается дифференцированием обеих частей уравнения, рассматривая y как функцию от x, а затем из полученного уравнения находится y`.
Пример 3. Найти производную от неявной функции x2 +3xy + y2 + 1 =0 и вычислить y` в точке (2; -1).
Решение. Дифференцируя по x, получаем: 
отсюда
. Подставим x =2, y = -1, получим 
.
В.7. Производные высших порядков
Производная 
называется производной 1-го порядка. Однако производная сама является функцией, которая также может иметь производную.
Производная n -го порядка называется производная от производной (n-1)- го порядка:
.
Обозначается: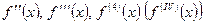 
и т.д.
Механический смысл 2-й производной: 2-ая производная пути по времени 
равна ускорению точки в момент t0.
В.9. Приложения производной
Правило Лопиталя
Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Другими словами, если имеется неопределенность 
или 
, то
Пример 4. Найти предел, используя правило Лопиталя: 
.
Решение. Имеем неопределенность вида . Применяя правило Лопиталя, получим:
= 
. Неопределенность вида по-прежнему сохраняется. Применим правило еще раз: = 
.
Ответ: 1.
