Решение. Так как величины  и
и  независимы, то незави- независимы также и величины
независимы, то незави- независимы также и величины  и
и  . Используя свойства дисперсии (дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых; постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат), получим
. Используя свойства дисперсии (дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых; постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат), получим
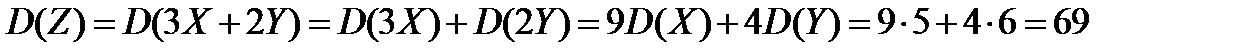 .
.
Случайные величины и независимы. Найти дисперсию случайной величины, если известно, что,.
Решение.
Так как величины  и
и  независимы, то независимы также и величины
независимы, то независимы также и величины  и
и  . Используя свойства дисперсии получим:
. Используя свойства дисперсии получим:
 .
.
№210 Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины X, заданной законом распределения:

Решение:
Дисперсию можно вычислить, исходя из ее определения, однако мы воспользуемся формулой
 ,
,
которая быстрее ведет к цели.
Найдем математическое ожидание  :
:

Напишем закон распределения 
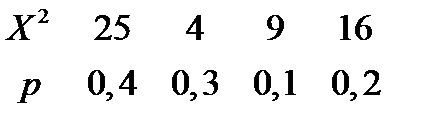
Найдем математическое распределение 

Найдем искомую дисперсию:
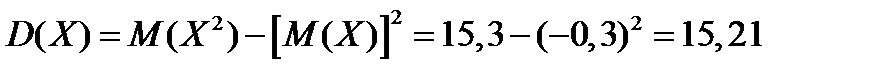 .
.
Найдем искомое отклонение:  .
.
№211 Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины  , заданной законом распределения:
, заданной законом распределения:
a) 
б) 
Решение:
Для вычисления дисперсии воспользуемся формулой:
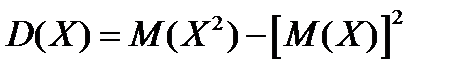
Найдем математическое ожидание 
а) 
б) 
Напишем закон распределения для  :
:
a) 

б) 
Найдем математическое ожидание 
а) 
б) 
Найдем искомую дисперсию:
а) 
б) 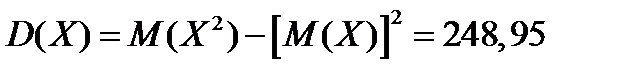
Найдем искомое среднее квадратическое отклонение:
a) 
б) 
№212 Дискретная случайная величина Х имеет только два возможных значения х1 и х2, причем равновероятных. Доказать, что дисперсия величины Х равна квадрату полуразности возможных значений;
 .
.
Решение:
найдем математическое ожидание Х, учитывая, что вероятности возможных значений  и
и  х2 и, следовательно, каждая из них равна ½;
х2 и, следовательно, каждая из них равна ½;
 .
.
Найдем математическое ожидание  ;
;
 ,
,
Найдем дисперсию Х:
 .
.
Найти дисперсию дискретной случайной величины —числа появлений события в пяти независимых испытаниях, если вероятность появления событий А в каждом испытании равна 0,2.
Решение.
Дисперсия числа появлений события в независимых испытаниях (с одинаковой вероятностью появления события в каждом испытании) равна произведению числа испытаний на вероятности появления и непоявления события:
 .
.
По условию,  ;
;  ;
;  .
.
Искомая дисперсия

Ответ: 0,8
Найти дисперсию дискретной случайной величины – числа отказов элемента некоторого устройства в десяти независимых опытах, если вероятность отказа элемента в каждом опыте равна 0,9.
Решение:
Дисперсия числа появлений события в независимых испытаниях(с одинаковой вероятностью появления события в каждом испытании) равна произведению числа испытаний на вероятности появления и непоявления события:
 .
.
По условию,  ;
;  ;
;  .
.
Искомая дисперсия

Ответ: 0,9
Рудченко Олег
№215 Найти дисперсию дискретной случайной величины 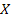 — числа появлений события
— числа появлений события 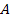 в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что
в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что  .
.
Решение.
Первый способ: Возможные значения величины 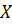 таковы:
таковы:  (событие не появилось),
(событие не появилось),  (событие появилось один раз) и
(событие появилось один раз) и 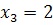 (событие появилось два раза).
(событие появилось два раза).
Найдем вероятности возможных значений по формуле Бернулли:
P2(0)=q2;  ; P2(2)=p2;
; P2(2)=p2;
Напишем закон распределения 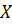 :
:
|
Найдём 

В силу условия  , т. е.
, т. е.  . Отсюда
. Отсюда  и, слеследовательно,
и, слеследовательно,  .
.
Искомая дисперсия

Второй способ: Воспользуемся формулой  . По условию,
. По условию,  ;
;  . Следовательно,
. Следовательно,  . Отсюда
. Отсюда  и, значит,
и, значит,  .
.
Найдем искомую дисперсию:

№216 Найти дисперсию дискретной случайной величины Х – числа появлений события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что М(Х)=0.9.
Решение.



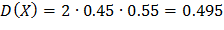
Ответ: 0.495.
№217 Производятся независимые испытания с одинаковой вероятностью появления события А в каждом испытании. Найти вероятность появления события А, если дисперсия числа появлений события в трех независимых испытаниях равна 0,63.
Решение:
Дисперсия равна:




p2-p+0,21=0

Решим квадратное уравнение.
Искомая вероятность появления события А равна:
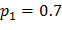

№218 Сумма вероятностей всех возможных значений дискретной случайной величины равна единице, поэтому вероятность того, что  примет значение
примет значение
 , равна
, равна 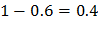
Напишем закон распределения Х:

| 
| 
|

| 
| 
|
{1}
Для отыскания  и
и  надо составить два уравнения, связывающие эти числа. С этой целью выразим известные математическое ожидание и дисперсию через
надо составить два уравнения, связывающие эти числа. С этой целью выразим известные математическое ожидание и дисперсию через  и
и  .
.
Найдём 

По условию,  , следовательно {2}
, следовательно {2} 
Для того, чтобы получить второе уравнение, выразим известную дисперсию через  и
и  .
.
Напишем закон распределения 

| 
| 
|

| 
| 
|
найдём 

Найдём дисперсию

Подставляя  , после элементарных преобразований получим
, после элементарных преобразований получим

Объединяя {2} и {3}, получим систему уравнений

Решив эту систему, найдём 2 решения
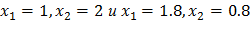
По условию 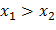 , поэтому задаче удовлетворяет лишь первое решение
, поэтому задаче удовлетворяет лишь первое решение  ,
,  {4}
{4}
Подставив {4} в {1}, получим искомый закон распределения

| 
| 
|

| 
| 
|
№219 Дискретная случайная величина X имеет только два возможных значения: x1 и x2, причем x1<x2. Вероятность того, что X примет значение x1, равна 0,2. Найти закон распределения X, зная математическое ожидание M(X)=2,6 и среднее квадратическое отклонение σ(X)=0,8.
Решение:
Напишем закон распределения Х (вероятность х2 получим из формулы о сумме вероятностей всех возможных значений дискретной случайной величины):

| 
| 
|

| 
| 
|
Нам известно математическое ожидание, тогда:

Так как 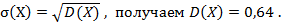 Т.е.
Т.е.  , отсюда
, отсюда 
Объединяя, получим систему уравнений (умножим каждое на 5):

Решивсистему, получим: 
Ответ:

| 
| 
|

| 
| 
|
№220 Дискретная случайная величина  имеет только три возможных значения:
имеет только три возможных значения:  ,
,  , причем
, причем  . Вероятности того, что
. Вероятности того, что  примет значения
примет значения 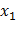 и
и  соответственно равны 0,3 и 0,2. Найти закон распределения
соответственно равны 0,3 и 0,2. Найти закон распределения
величины  , зная ее математическое ожидание
, зная ее математическое ожидание  и дисперсию
и дисперсию  .
.

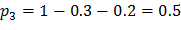

| 
| 
| 
|

| 
| 
| 
|







| 
| 
| 
|

| 
| 
| 
|
№221 Брошены n игральных костей. Найти дисперсию суммы числа очков, которые могут появиться на всех выпавших гранях.
Решение:
Обозначим через X дискретную случайную величину— сумму числа очков, которые выпадут на всех гранях, через  — число очков, выпавших на грани i -й кости. Тогда
— число очков, выпавших на грани i -й кости. Тогда
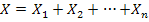
Очевидно, все величины X имеют одинаковое распределение, следовательно, одинаковые числовые характеристики и, в частности, одинаковые дисперсии,
т. е.
 . (*)
. (*)
Так как рассматриваемые случайные величины независимы, то дисперсия их суммы равна сумме дисперсий слагаемых:
 .
.
В силу (*) получим
 . (**)
. (**)
Таким образом, достаточно вычислить дисперсию случайной величины 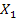 , т. е. дисперсию числа очков, которые могут выпасть на «первой» кости.
, т. е. дисперсию числа очков, которые могут выпасть на «первой» кости.
Напишем закон распределения 
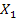
| ||||||
| p | 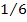
| 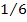
| 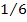
| 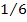
| 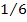
| 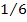
|

Найдем 
Напишем закон распределения 
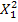
| ||||||
| p | 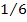
| 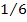
| 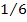
| 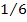
| 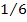
| 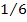
|
Найдем  и
и 

 (***)
(***)
Найдем искомую дисперсию, для чего подставим (***) в (**):

Ответ:  .
.
№222 Вероятность наступления события в каждом испытании равна p  . Испытания производятся до тех пор, пока событие не наступит. Найти:
. Испытания производятся до тех пор, пока событие не наступит. Найти:
А) математическое ожидание дискретной случайной величины X – числа испытаний, которые надо произвести до появления события;
Б) дисперсию величины X.
Решение.
А) Составим закон распределения величины X – числа испытаний, которые надо произвести, пока событие не наступит:

| 
| 
| 
| … | 
| … |

| 
| 
| 
| … | 
| … |








