Решение:
Пусть Х – дискретная случайная величина, заданная законом распределения:
Обозначим наименьшее и наибольшее значения 
соответственно через 
и 
. Тогда 
Итак, 
Аналогично можно вывести, что 
Объединяя, получим 
Ч.Т.Д.
Дискретная случайная величина принимает положительных значений,, …, с вероятностями, равными соответственно,, …,. Предполагая, что возможные значения записаны в возрастающем порядке, доказать, что
Решение:
Принимая во внимание, что 
и 
, получим
Так как по условию возможные значения 
записаны в возрастающем порядке, т. е.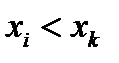 
, то
и 
.
Следовательно,
Предположение доказано.
Доказать, что если случайные величины,,… независимы, положительны и одинаково распределены, то
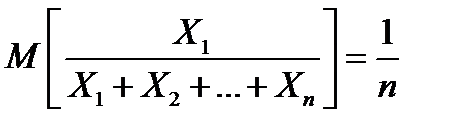
Решение:
Введем в расмотрение случайные величины
, 
, …, 
.(*)
Заметим, что знаменатели этих дробей не могут быть равными нулю, поскольку величины 
(
) положительны.
По условию, величины 
одинаково распределены, поэтому 
также одинаково распределены и, следовательно, имеют одинаковые числовые характеристики, в частности, одинаковые математические ожидания:
(**)
Легко видеть, что 
, следовательно,
.
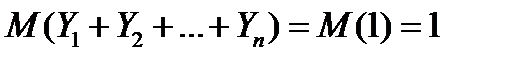Математическое ожидание суммы равно сумме математических ожиданий слагаемых, поэтому
.
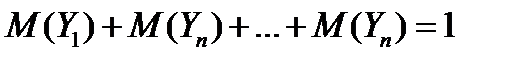В силу (**) имеем 
. Отсюда 
.
Учитывая (*), окончательно получим
.
Что и требовалось доказать.
Доказать, что если случайные величины,,, независимы, положительны и одинаково распределены, то
.
Решение:
Введем в расмотрение случайные величины
, 
, …, 
.(*)
Заметим, что знаменатели этих дробей не могут быть равными нулю, поскольку величины 
(
) положительны.
По условию, величины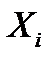 
одинаково распределены, поэтому 
также одинаково распределены и, следовательно, имеют одинаковые числовые характеристики, в частности, одинаковые математические ожидания:
(**)
Легко видеть, что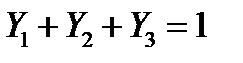 
, следовательно,
.
Математическое ожидание суммы равно сумме математических ожиданий слагаемых, поэтому
.
В силу (**) имеем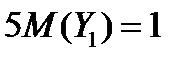 
. Отсюда 
.
Учитывая (*), окончательно получим
.
Что и требовалось доказать.
№207 Найти математическое ожидание дискретной случайной величины 
, распределенной по закону Пуассона:
Решение:
По определению математического ожидания для случая, когда число возможных значений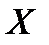 
есть счетное множество,
.
Учитывая, что при 
первый член суммы равен нулю, примем в качестве наименьшего значения 
единицу:
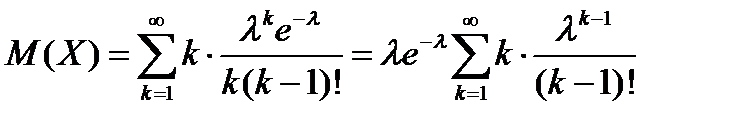
Положив 
, получим
Принимая во внимание, что 
, окончательно имеем
.
Итак,
,
т.е. математическое ожидание распределения Пуассона равно параметру этого распределения λ.
