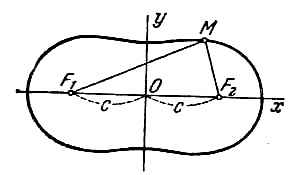
Глава 26. Уравнение некоторых кривых, встречающихся в математике и ее приложениях

		Составить уравнение геометрического места точек, произведение расстояний от которых до двух данных точек F₁(-c; 0), F₂(c; 0) есть постоянная величина a². Такое геометрическое место точек называется овалом Кассини (см. рис.).
		Составить уравнение геометрического места точек, произведение расстояний от которых до двух данных точек F₁(-а; 0), F₂(а; 0) есть постоянная величина а². Такое геометрическое место точек называется лемнискатой (см. рис.). (Уравнение лемнискаты сначала найти непосредственно, потом – рассматривая ее как частный вид овала Кассини). Составить также уравнение лемнискаты в полярных координатах, совмещая полярную ось с положительной полуосью Ох и полюс с началом координат.
		Составить уравнение геометрического места оснований перпендикуляров,опущенных из начала координат на прямые, отсекающие от координатного угла треугольники постоянной площади S.
		Доказать, что геометрическое место точек задачи 703 есть лемниската (см. задачу 702).
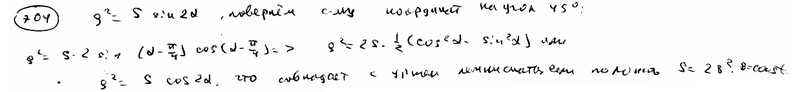
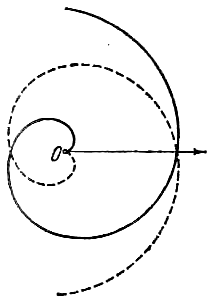
		Луч а, в начальном положении совпадающий с полярной осью, вращается вокруг полюса О с постоянной угловой скоростью 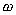. Составить в даной системе полярных координат уравнение траектории точки М, которая, имея начальное положение в О, движется по лучу а равномерно со скоростью v (спираль Архимеда, (см. рис.).
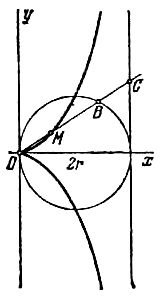
		Даны прямая и окружность радиуса r, которая проходит через начало координат О и касается данной прямой. Из точки О проведен луч, пересекающий данную окружность в точке В и данную прямую в точке С, на котором отложен отрезок ОМ=ВС (см. рис.). При вращении луча длина отрезка ОМ меняется и точка М описывает кривую, называемую циссоидой. Составить уравнение циссоиды.
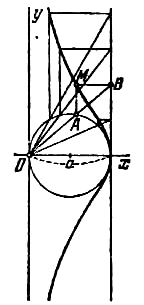
		Даны прямая x=a (a>0) и окружность радиуса а, проходящая через начало координат О и касающаяся данной прямой. Из точки О проведен луч, пересекающий окружность в точке А и данную прямую в точке В. Из точек А и В проведены прямые, параллельные соответственно осям Оу и Ох (см. рис.). Точка М пересечения этих прямых при вращении луча описывает кривую, называемую верзьерой. Составить ее уравнение.
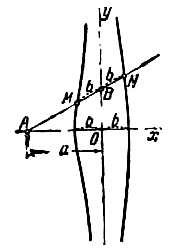
		Из точки А(-а; 0), где а>0, проведен луч АВ (см. рис.), на котором по обе стороны от точки В отложены отрезки BM, BN одинаковой длины b (b=const). При вращении луча точки M и N описывают кривую, называемую конхоидой. Составить ее уравнение сначала в полярных координатах, помещая полюс в точку А и направляя полярную ось в положительном направлении оси Ох, а затем перейти к данной системе декартовых прямоугольных координат.
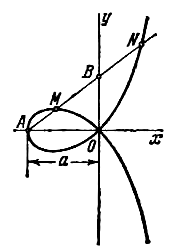
		Из точки А(-а; 0), где a>0, проведен луч АВ (см. рис.), на котором по обе стороны от точки В отложены отрезки BM и BN, равные ОВ. При вращении луча точки M и N описывают кривую, называемую строфоидой. Составить ее уравнение сначала в полярных координатах, помещая полюс в точке А и направляя полярную ось в положительном направлении оси Ох, а затем перейти к данной системе декартовых прямоугольных координат.
		Из начала координат проведен луч, пересекающий данную окружность 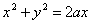(а>0) в точке В (см. рис.); на луче по обе стороны от точки В отложены равные между собой отрезки BM и BN постоянной длины b. При вращении лча точки M и N описывают кривую, называемую улиткой Паскаля (см. рис.). Составить ее уравнение сначала в полярных координатах, совмещая полю с началом координат и полярную ось с положительной полуосью Ох, а затем перейти к данной системе декартовых прямоугольных координат.
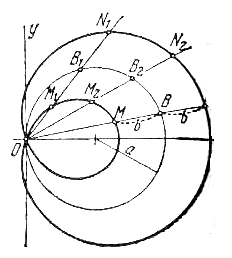
		Отрезок длины 2а движется так, что его концы все время находятся на координатных осях. Составить уравнение траектории основания М перпендикуляра, опущенного из начала координат на отрезок (см. рис.), сначала в полярных координатах, совмещая полюс с началом координат и полярную ось с положительной полуосью Ох, а затем перейти к данной системе декартовых прямоугольных координат. Точка М описывает кривую, называемую четырехлепестковой розой.
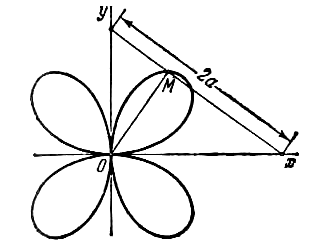
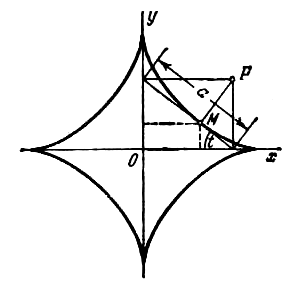
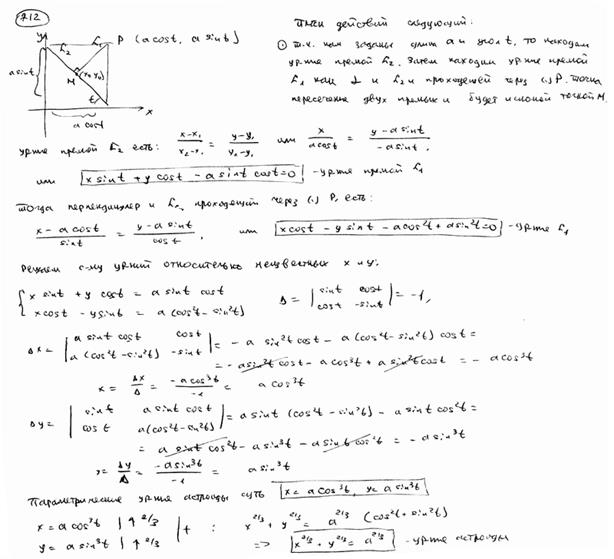
		Отрезок длины а движется так, что его концы все время находятся на координатных осях. Через концы отрезка проведены прямые, параллельные координатным осям, до их взаимного пересечения в точке Р. Составить уравнение траектории основания М перпендикуляра, опущенного из точки Р на отрезок. Эта траектория называется астроидой.
		Из точки В пересечения луча ОВ с окружностью опущен перпендикуляр ОМ. Вывести уравнение траектории точки М сначала в полярных координатах, совмещая полюс с началом координат и полярную ось с положительной полуосью Ох, а затем перейти к данной системе декартовых прямоугольных координат.
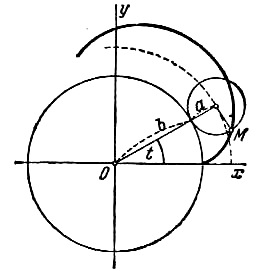
		Нить, намотанная на окружность 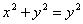, разматывается так, что в точке В,где нить отделяется от окружности, она остается касательной к ней (см. рис.). Найти параметрические уравнения линии, описываемой концом нити, если начальным положением конца является точка А(а; 0), где а>0. Линия, о которой идет речь, называется эвольвентой окружности.
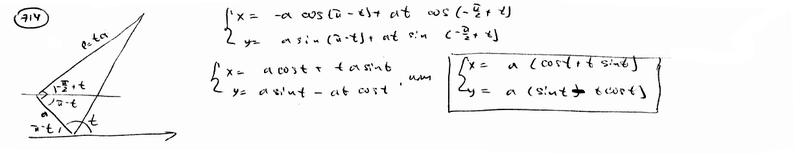
		Круг радиуса а катится без скольжения по оси Ох. Траектория некоторой точки М окружности этого круга называется циклоидой (см. рис.). Вывести параметрические уравнения циклоиды, принимая в качестве параметра t угол, на который поворачивается катящаяся окружность вокруг своего центра; считать при этом, что в начальный момент (t=0) точка М находится в начале координат. Исключить параметр t из полученных уравнений.
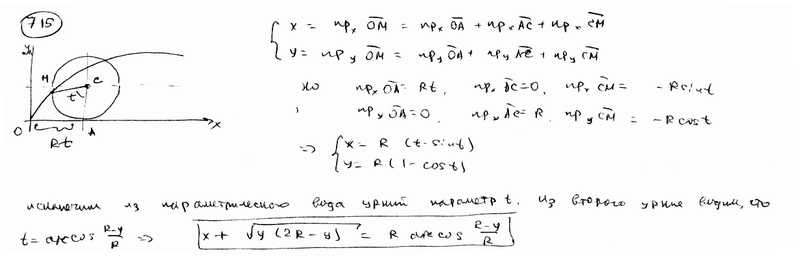
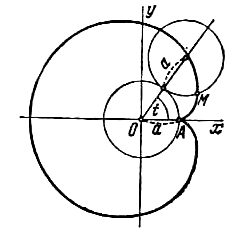
		Круг радиуса а катится без скольжения по окружности 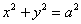, оставаясь вне ее. Траектория некоторой точки М окружности катящегося круга называется кардиоидой (см. рис.). Вывести параметрические уравнения кардиоиды, выбирая в качестве параметра t угол наклона к оси Ох радиуса неподвижной окружности, проведенного в точку касания с подвижной. Считать при этом, что в начальный момент (t=0) точка М находится справа на оси Ох. Перейти к полярным координатам при условии, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в точке А. Доказать, что кардиоида есть частный вид улитки Паскаля (см. задачу 710).
		Круг радиуса а катится без скольжения по окружности 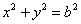, оставаясь вне ее. Траектория некоторой точки М окружности катящегося круга называется эпициклоидой (см. рис.). Вывести параметрические уравнения эпициклоиды, выбирая в качестве параметра t угол наклона к оси Ох радиуса неподвижной окружности, проведенного в точку касания с подвижной; считать при этом, что в начальный момент (t=0) точка М находится справа на оси Ох. Доказать, что кардиоида (см. задачу 716) есть частный вид эпициклоиды.
		Круг радиуса а катится без скольжения по окружности 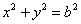, оставаяь внутри нее. Траектория некоторой точки М окружности катящегося круга называется гипоциклоидой (см. рис.). Вывести параметрические уравнения гипоциклоиды, выбирая в качестве параметра t угол наклона к оси Ох радиуса неподвижной окружности, проведенного в точку касания с подвижной; считать при этом, что в начальный момент (t=0) точка М находится справа на оси Ох. Доказать, что астроида (см. задачу 712) есть частный вид гипоциклоиды.