Генерация и рекомбинация неравновесных

Носителей. Время жизни

В момент генерации неравновесные носители, как правило, обладают большей энергией, чем равновесные. Однако в дальнейшем в результате рассеяния на фононах и дефектах кристаллической решетки кинетическая энергия неравновесных носителей быстро уменьшается до нормальных значений (рис. 6.1, а). Обычно это время порядка 10^-10 с. Таким образом, можно считать, что избыточные носители практически сразу после возбуждения оказываются распределенными по энергиям, так же, как и равновесные носители, и результатом действия возбуждающего фактора является только рост концентрации носителей.

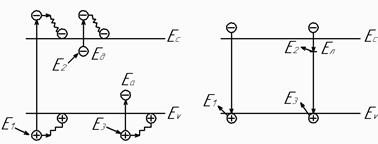
а) б)

Рис. 6.1. Генерация (а) и рекомбинация (б) неравновесных носителей

Как было показано выше (п.5.3), концентрация равновесных носителей однозначно определяется положением уровня Ферми. Очевидно, что концентрация неравновесных носителей уже не может описываться с помощью тех же формул. Однако в большинстве случаев оказывается удобным использовать аналогичные выражения:

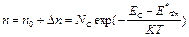, (6.1)

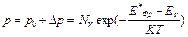, (6.2)

где n ₀, p ₀− равновесная концентрация;

Δ n, Δ р − избыточная концентрация носителей;

E^*_Ф_n, E^*_Ф_p − квазиуровни Ферми для электронов и дырок.

Необходимо отметить, что введение понятия о квазиуровне Ферми является формальным приемом и не характеризует равновесного состояния в системе.

Процесс генерации носителей характеризуется скоростью генерации g_n, когда за время dt в объеме dV ионизирующий фактор создает g_n dVdt электронов. Если объем единичный, то можно записать выражение:

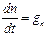(6.3)

В выражении (6.3) не отражен процесс рекомбинации. С ростом избыточной концентрации электронов, скорость рекомбинации R_n также возрастает, она пропорциональна избыточной концентрации:

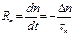, (6.4)

где τ_n – среднее время жизни электронов.

С учетом (6.3) и (6.4) можно записать выражение:

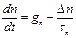. (6.5)

Физический смысл τ_n можно определить, решив уравнение (6.5) для случая выключения ионизирующего фактора. При g_n (t) = 0

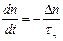. (6.6)

Решение последнего уравнения имеет вид:

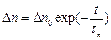, (6.7)

где Δ n ₀ − избыточная концентрация электронов при t =0.

Из этого решения видно, что процесс рекомбинации описывается уравнением релаксации и τ_n является временем релаксации.

Соотношения, аналогичные (6.3)-(6.7), можно записать и для дырок.

Способность дырки к захвату электрона при рекомбинации характеризуется параметром эффективное сечение захвата S_n. Это часть плоскости, переходящей через дырку, где происходит захват электрона. Среднее время жизни, равное времени пробега электрона до его захвата, можно выразить

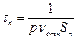, (6.8)

где 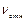− скорость электрона относительно дырки.

В процессе захвата и рекомбинации могут участвовать как свободные дырки в валентной зоне, так и «локализованные» на различных примесных уровнях, дефектах (ионы). Для каждого случая среднее время жизни электрона будет определяться параметрами (6.8).

Свободные носители заряда, диффундируя в объеме полупроводника за время жизни τ перемещаются на расстояние L, которое называют диффузионной длиной:

L =√ Д τ, (6.9)

здесь Д − коэффициент диффузии носителей, связанный с их подвижностью μ соотношением Эйнштейна:

Д 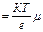. (6.10)

С точки зрения механизма протекания различают межзонную рекомбинацию, рекомбинацию через примесные центры (центры рекомбинации) (рис. 6.1, б) и поверхностную рекомбинацию. Межзонная рекомбинация в условиях теплового равновесия характеризуется скоростью R ₀, которая по определению должна быть равна скорости генерации носителей:

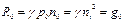, (6.11)

где γ =g ₀ /n_i ²− коэффициент рекомбинации.

В случае работы ионизирующего фактора можно записать:

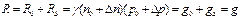, (6.12)

где R − суммарная скорость рекомбинации;

g − суммарная скорость генерации;

R _Δ – скорость рекомбинации неравновесных носителей.

g _Δ − скорость генерации неравновесных носителей.

В случае низкого уровня возбуждения полупроводника ионизирующим фактором Δ n Δ p<<n ₀ p ₀с учетом условий Δ n= Δ p и γ=g ₀ /n_i² можно записать:

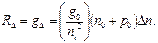(6.13)

Здесь скорость рекомбинации избыточных носителей пропорциональна их концентрации. Такую рекомбинацию называют линейной. Время жизни носителей для линейной рекомбинации составляет

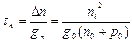. (6.14)

При высоком уровне возбуждения Δ p Δ n>>p ₀ n ₀ последние выражения примут иную форму:

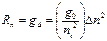, (6.15)

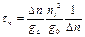. (6.16)

Скорость рекомбинации избыточных носителей пропорциональна квадрату их концентрации, а время жизни неравновесных носителей обратно пропорциональна ему. Такую рекомбинацию называют квадратичной.

При каждом акте рекомбинации электрона и дырки выделяется энергия, равная энергетическому промежутку между уровнями этих частиц (см. рис. 6.1, б). Эта энергия может выделяться либо в виде кванта света (излучательная рекомбинация), либо в виде тепловой энергии (фонона), передаваемой атомам решетки (безызлучательная рекомбинация). Как показывают исследования, излучательная рекомбинация играет относительно малую роль в реальных полупроводниках, за исключением полупроводников с малой шириной запрещенной зоны и с прямыми межзонными переходами. Прямым переходом называется переход электрона из минимума зоны проводимости в максимум валентной зоны, если эти экстремумы имеют одинаковое значение волнового вектора к.

Для полупроводников с широкой запрещенной зоной основным механизмом, ответственным за рекомбинацию, является безызлучательная рекомбинация через примесные уровни. Однако и в таких полупроводниках можно достичь относительно высокого уровня излучательной рекомбинации. Как видно из (6.14) и (6.16), необходимо повышение концентрации избыточных носителей в полупроводнике и увеличение степени его генерирования.

Рекомбинация через локальные уровни. Механизм этой рекомбинации состоит в том, что электрон из зоны проводимости сначала переходит на локальный уровень Е_л в запрещенной зоне, а затем на свободный уровень в валентной зоне (см. рис. 6.1, б). Такая двухступенчатая рекомбинация часто оказывается более вероятной, чем непосредственная рекомбинация электрона и дырки. Локальные уровни в запрещенной зоне полупроводника могут служить эффективными центрами рекомбинации, если они расположены вдали от зоны проводимости и валентной зоны, т.е. являются глубокими уровнями – ловушками. Мелкие уровни играют роль уровней прилипания: они постоянно обмениваются электронами с ближайшей зоной.

Теория рекомбинации через ловушки была разработана Холлом, Шокли и Ридом для ловушек одного уровня, если Δ n≈ Δ p. При таких допущениях было получено выражение для времени жизни неравновесных носителей:

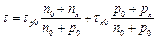, (6.17)

где n_л, р_л − равновесные концентрации носителей в случае совпадения Е_л и Е_ф;

τ_n ₀, τ_p ₀ − время жизни носителей в зонах, когда все ловушки для них свободны.

Проведя анализ этой формулы и считая, что τ_n ₀, τ_p ₀ имеют один порядок, можно выделить три предельных случая.

1. Сильно легированный n-полупроводник, n ₀ >>p ₀, n_л. Вследствие большой концентрации электронов в зоне проводимости, все ловушки оказываются занятыми электронами. В случае освобождения ловушки она тут же “заселяется” дыркой. Этот процесс и определяет время жизни носителей:

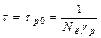, (6.18)

где N_л − концентрация ловушек;

γ_p − коэффициент захвата дырки.

2. Сильно легированный p-полупроводник, p ₀ >>n ₀, n_л. Ситуация, аналогичная предыдущей, только освобожденные ловушки заселяются электронами.

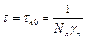. (6.19)

В первых двух случаях время жизни носителей зависит от концентраций ловушек и коэффициентов захвата, поэтому слабо зависит от температуры.

3. Сильно легированный полупроводник, n ₀ ≈ p _0.Уровень Ферми приближается к середине запрещенной зоны ближе, чем Е_л, и, следовательно n ₀ <<n_л, p ₀ <<р_л. Тогда выражение (6.17) примет вид:

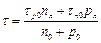. (6.20)

В этом случае время жизни зависит от концентрации равновесных носителей, а следовательно, и от температуры. Нетрудно заметить, что время жизни достигает максимума в случае собственного полупроводника, когда p ₀ =p ₀ =n_i

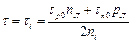. (6.21)

Поверхностная рекомбинация. На поверхности полупроводника имеется значительное количество поверхностных дефектов, которые могут являться эффективными центрами рекомбинации. Поэтому поверхностная рекомбинация протекает особенно быстро и в тонких пленках может преобладать над объемной концентрацией.

В результате поверхностной рекомбинации концентрация носителей на поверхности уменьшается, что приводит к их диффузии из объема полупроводника. Чем выше интенсивность поверхностной рекомбинации, тем больше скорость перемещения носителей к поверхности. В этой связи в качестве характеристики интенсивности поверхностной рекомбинации принята скорость s, равная средней скорости, с которой носители движутся из объема к поверхности. Величина скорости поверхностной рекомбинации зависит от характера обработки и состояния поверхности и меняется в диапазоне 10²–10⁴см/с. Процессы поверхностной рекомбинации могут играть значительную (часто негативную) роль в работе полупроводниковых, особенно оптоэлектронных приборов.

Уравнения непрерывности

Известно, что изменение концентрации неравновесных носителей может происходить в результате диффузии и дрейфа носителей, за счет градиента концентрации и электрического поля, генерации носителей и их рекомбинации. Можно установить некоторую закономерность изменения концентрации неравновесных носителей во времени и по объему полупроводника.

Для того, чтобы определить изменение концентрации неравновесных носителей, необходимо учесть все вышеперечисленные факторы:

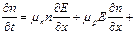Д _n 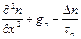, (6.22)

где Е – напряженность поля.

В случае если неравновесным носителями заряда являются дырки, уравнение непрерывности примет вид:

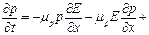Д _р 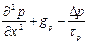(6.23)

В общем случае, когда концентрация электронов зависит от всех трех координат, уравнение непрерывности имеет вид:

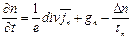, (6.24)

где

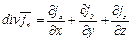. (6.25)

Уравнения (6.22) и (6.23) описывают влияния всех перечисленных факторов на концентрацию носителей и, если какие-либо факторы отсутствуют, уравнения непрерывности упрощаются. Так, например, если Е=const, первый член уравнения равен нулю, если Е= 0, то два первых члена обращаются в нуль и т.д. При условии отсутствия всех факторов dn/dt =0, что говорит о постоянстве концентрации носителей.

Рассмотренные уравнения (6.22) и (6.23) относятся к легированным полупроводникам, где n>>p или p>>n, а Δ n<<n ₀, Δ p<<p _0.В этом случае Δ n= Δ p и объемный заряд в полупроводнике отсутствует. Однако в случае полупроводников с проводимостью, близкой к собственной, в большинстве случаев это условие не выполняется. В собственных полупроводниках неравновесная концентрация обычно соизмерима с равновесной, и это приводит к нарушению условия электронейтральности. В полупроводнике появляется объемный заряд и связанное с ним электрическое поле.

В этом случае приближение Δ p = Δ n может быть сохранно для всех членов уравнения непрерывности, за исключением того, который содержит dE/dx. Этот член должен учитывать изменение электрического поля, вызванное объемным зарядом. Используя уравнение Пуассона, получим выражение:

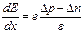. (6.26)

Проведя еще некоторые преобразования, можно получить уравнение непрерывности для данного случая в виде:

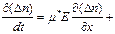Д 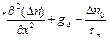, (6.27)

где Д ^* − эффективный коэффициент диффузии;

µ^* − эффективная подвижность носителей заряда.

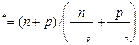, (6.28)

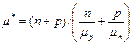. (6.29)

Таким образом, в случае, когда необходимо учитывать объемный заряд, создаваемый неравновесными носителями, вид уравнения непрерывности остается прежним, однако подвижность и коэффициент диффузии носителей заряда становятся переменными величинами.