Скорость электронов в твердых телах и, в частности, в полупроводниках J состоит из тепловой JТ и дрейфовой составляющих Jд
J = JТ + Jд. (6.52)
Тепловая составляющая скорости электрона определяется структурой кристалла и температурой, дрейфовая составляющая зависит от напряженности электрического поля E
Jд = μE. (6.53)
Выше (п. 5.1) мы установили, что подвижность носителей заряда не зависит от напряженности электрического поля. Концентрация носителей также не зависит от напряженности поля (п. 5.3), следовательно, закон Ома имеет линейный характер.
Электрические поля, в которых выполняются эти закономерности, называются слабыми. Очевидно, что электрические поля, которые мы рассматривали до сих пор относятся к слабым. В обычных условиях выполняется соотношение
JТ >> Jд. (6.54)
Это критерий слабого поля.
Оценим дрейфовую и тепловую скорости электрона в германии. В чистом германии при комнатной температуре JТ ≈2,5∙105 м/с, а Jд ≈39 м/с при Е = 100 В/м, т.е. соотношение (6.54) выполняется. В слабых полях скорость электрона определяется тепловой компонентой, поэтому для простоты мы использовали при расчетах проводимости и подвижности именно тепловую скорость.
При увеличении направленности электрического поля дрейфовая скорость растет и при некотором критическом значении – Eкр она достигает величины Jд ≈0,1 JТ. Это критерий сильного поля. Теперь необходимо учитывать влияние электрического поля на подвижность и концентрацию носителей. На основании (6.53) можно записать
D J = μЕ. (6.55)
Отсюда видно, что измерение скорости будет зависеть не только от напряженности поля, но и от подвижности носителей.
Рассмотрим влияние сильного поля на подвижность при различных механизмах рассеяния. Как известно из п. 5.2, в случае электрон-фононного рассеяния µф ~ J -1/2. С учетом (6.55) в сильных полях
Δ υ ~ Е -1/2. (6.56)
При электрон-ионном рассеянии µu ~ J 3/2. В сильных полях
Δ υ ~ Е 3/2. (6.57)
Сильное поле, увеличивая скорость электрона, по-разному будет влиять на время релаксации. В первом случае оно будет уменьшать τ, а второй – увеличивать ее. Поскольку суммарная подвижность определяется из выражения
, (6.58)
то, учитывая рис. 5.2, а, можно сделать вывод о зависимости μ (Е). Она отображена на рис. 6.5, а.
|
|
|
|
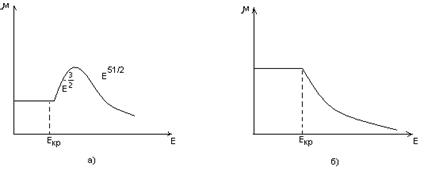
Рис. 6.5. Зависимость подвижности носителей от напряженности поля: а – электрон-фононное и электрон-ионное рассеяние; б – электрон-фононное рассеяние
Следует отметить, что при более высоких температурах преобладает электрон-фононное рассеяние, а при низких – электрон-ионное рассеяние. В случае малой концентрации ионов подвижность уменьшается с ростом напряженности поля, поскольку здесь преобладает электрон-фононное рассеяние (см. рис. 5.6, б)
Очевидно, что уменьшение подвижности носителей должно приводить к уменьшению электропроводности. Однако этот эффект удается наблюдать не всегда, поскольку в большинстве практических случаев рост поля приводит к резкому увеличению электропроводности за счет значительного повышения концентрации носителей.
В сильных полях работают эффекты, связанные с ростом концентрации носителей при увеличении напряженности поля. К ним, в первую очередь, относятся термоэлектронная ионизация донорной примеси, электростатическая ионизация (эффект Зинера) и ударная ионизация (лавинный пробой).
Термоэлектронная ионизация (эффект Френкеля) в полупроводниках протекает следующим образом. Под действием сильного электрического поля потенциальный барьер донорного атома искажается, в результате чего высота потенциального направления уменьшается на некоторую величину D W. Энергия активации примеси в этом случае равна D Eд- D W, а концентрация носителей по сравнению с равновесной n 0 будет больше
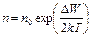. (6.59)
Величина D W численно равна потенциальной энергии электрона в точке Х 0, где кривая потенциального барьера достигает максимума, как показывает расчет:
, (6.60)
где ε – диэлектрическая проницаемость кристалла. С учетом (6.59) и (6.60) можно записать выражения для электропроводимости
, (6.61)
где а – коэффициент пропорциональности.
Это выражение называют законом Френкеля.
Для более слабых полей теория приводит к закону Пула
σ = σ 0 exp[ α (E - Eкр)], (6.62)
где α – коэффициент, зависящий от температуры.
Ударная ионизация (рис. 6.6) происходит в полях, способных сообщить свободному электрону энергию, достаточную для того, чтобы он смог ионизировать атом полупроводника. Если при этом ионизирующий электрон остается в зоне проводимости, процесс роста концентрации приобретает лавинный характер.
Различают высоковольтную и низковольтную ударные ионизации. В первом случае электрон приобретает необходимую энергию на длине одного свободного пробега. При низковольтной ионизации такая энергия накапливается постепенно.
|
|
|
|
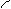
Рис. 6.6. Процессы в сильных полях: а – переходы электронов, 1 – ударная ионизация,
2 – туннельный переход, б – изменение электропроводимости, участки: О – Ома,
Ф – Френкеля, У – ударной ионизации, З – Зенера, П – пробой
Следует отметить, что рассмотренный эффект зависит от температуры и проявляется лишь тогда, когда не все атомы примеси ионизированы за счет термического возбуждения.
Электростатическая ионизация связана с туннельным прохождением электрона из валентной зоны в зону проводимости (рис. 6.6, а)
Вероятность туннельного просачивания электронов через потенциальный барьер w сильно зависит от ширины запрещенной зоны и напряженности приложенного поля. Для переходов типа 2 расчет приводит к следующему выражению
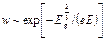. (6.63)
Оценка по этой формуле показывает, что при Eg ≈1 эВ вероятность w становиться заметной при E ≈109 В/м. Из (6.63) видно, что w, а следовательно, и концентрация носителей заряда генерируемых сильным полем, не зависит от температуры. Этим эффект Зеннера отличается от эффекта Френкеля и ударной ионизации.
Увеличение концентрации носителей заряда в результате описанных эффектов не носит на первых порах лавинного характера, т.к. оно ограничивается процессом рекомбинации, протекающим с тем более высокой скоростью, чем больше образуется носителей. Однако в очень сильных полях (107– 109В/м) начинается лавинное нарастание числа носителей, сопровождающееся пробоем полупроводника.
На рис. 6.6, б показана качественная кривая роста удельной проводимости с повышением напряженности поля и указаны приблизительные интервалы для различных механизмов роста.
