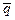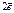Электропроводность металлов и сплавов

В металлах концентрация электронного газа максимальна и поэтому практически не зависит от температуры. Вследствие этого температурная зависимость электропроводности металлов определяется температурной зависимостью подвижности электронов вырожденного электронного газа (п.5.2). В достаточно чистом металле, где концентрация примесей невелика, подвижность, вплоть до весьма низких температур, определяется электрон-фононным рассеянием.

Подставив (5.24) в выражение (5.15), получим зависимость

σ ~ 1/ Т, (5.60)

или для удельного сопротивления

ρ = 1/ σ = αТ, (5.61)

где α – температурный коэффициент сопротивления.

В области низких температур концентрация фононного газа пропорциональна Т ³, поэтому длина свободного пробега

λ ~ Т^-3, (5.62)

а средний импульс фононов оказывается гораздо меньше импульса электрона.

В итоге эффективная длина свободного пробега электрона оказывается в сто раз меньше, а уточненные зависимости для ρ и σ примут вид

σ ~ Т ^-5, ρ ~ Т ⁵. (5.63)

В области температур, близких к абсолютному нулю, необходимо учитывать рассеяние электронов на примесных атомах. В этом случае, согласно (5.23), подвижность электронов не зависит от температуры и называется остаточным сопротивлением ρ ₀

ρ = ρ_Т + ρ ₀, (5.64)

где ρ_Т – доля температурнозависимого удельного сопротивления.

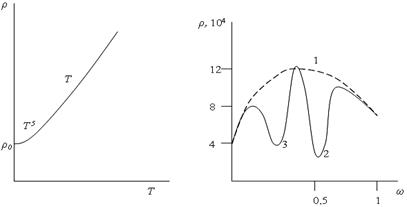
Последнее выражение называют правилом Матиссена, его график представлен на рис. 5.7, а.

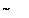
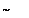
а) б)

Рис. 5.7. Удельное сопротивление: а – металлы; б – сплавы;

1 – неотожженный состав; 2 – CuAu; 3 – Cu₃Au

Картина удельного сопротивления для сплавов оказывается гораздо более сложной, чем для чистых металлов. Она определяется химическим взаимодействием между компонентами сплава. Если химическое взаимодействие компонентов отсутствует, то примесные атомы создают дополнительные центры рассеяния электронов, искажая кристаллическую решетку металла. В этом случае удельное сопротивление сплава значительно выше, чем у чистых металлов. Для удельного сопротивления бинарных сплавов можно привести соотношение Нордгейма

ρ_спл = β [ ω (1- ω)], (5.65)

где β – коэффициент пропорциональности;

ω, 1- ω – доли металлов, образующих сплав.

Очевидно, что ρ_спл имеет максимум при ω = ½ (рис. 5.7, б, график 1).

Однако, если атомы сплавов могут вступать в реакцию и образовывать интерметаллические соединения, то появляются области с пониженным удельным сопротивлением (рис. 5.7, б, 2, 3). Данный эффект объясняется упорядочением структуры сплава в этих областях и, как следствие, возрастанием длины свободного пробега электрона.

Сверхпроводимость

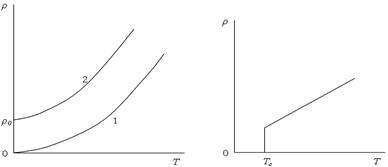
В 1911 г. голландский ученый Камерлинг-Оннес проводил эксперименты по исследованию сопротивления материалов при низких температурах. Он в 1908 г. получил жидкий гелий и теперь имел возможность охлаждать твердые тела до рекордно низких температур 4,2 К. При охлаждении ртути до температуры жидкого гелия ее сопротивление скачком падало до нуля (рис. 5.8, б). Это был новый физический эффект, который получил название сверхпроводимости.

а) б)

Рис. 5.8. Температурная зависимость: а – проводник; б – сверхпроводник;

Т_С – критическая температура; 1 – идеальный кристалл; 2 – реальный кристалл

Здесь необходимо сказать несколько слов о результатах, которых ожидали от таких экспериментов. Согласно существовавшим представлениям о механизмах электропроводности, бездефектный (идеальный) кристалл с понижением температуры должен был постепенно терять электросопротивление до нуля (рис. 5.8, а). Однако в эксперименте с ртутью исчезновение сопротивления осуществлялось не постепенно, а скачком в температурном интервале в несколько сотых долей градуса. Как выяснилось впоследствии, такое состояние при низких температурах наблюдается примерно у половины металлических элементов, большого числа металлических соединений, у ряда полупроводников и оксидов (табл. 5.1)

Таблица 5.1

Температура сверхпроводящего перехода

Материал НТСП	Т_С, К	Материал ВТСП	Т_С, К
Al	1,19	La_2-xSr_xCuO₄
Hg	4,15	Tl₂BaCuO₆
Pb	7,2	YBa₂Cu₃O₇
Sn	3,72	Bi₂Sr₂Ca₂Cu₃O₁₀
TiO₂	3,44	Tl₂Ba₂CaCu₂O₈
MoN		HgBa₂CaCu₂O₆
Nb₃Ge	23,4	HgBa₂Ca₂Cu₃O₈

Многие металлы не переходили в сверхпроводящее (СП) состояние до самых низких температур (все ферромагнетики, Ag, Au), ряд других элементов переходит в сверхпроводящее состояние только под давлением (Ge, Se, P). Эти элементы и соединения названы низкотемпературными сверхпроводниками (НТСП). Они размещены в первой колонке табл. 5.1.

В 1986 г. Г. Беднорцем и К. Миллером был открыт новый класс высокотемпературных сверхпроводников (ВТСП). Примеры таких материалов приведены во второй колонке таблицы.

В дальнейшем было установлено самое главное: эффект сверхпроводимости не ограничивается обращением сопротивления в нуль при температуре перехода, он включает в себя ряд не менее важных эффектов, каждый из которых может быть использован в микроэлектронике.

К таким эффектам и явлениям следует отнести: эффект Мейсснера-Оксенфельда – выталкивание магнитного поля из сверхпроводника; квантование магнитного потока в сверхпроводниковом кольце; эффекты Джозефсона; вихри Абрикосова – кванты магнитного потока и т.д.

Ограниченные рамками данной книги, мы не можем подробно осветить эти вопросы и поэтому отсылаем любознательного читателя к дополнительной литературе, например, [4], [11] и т.д.

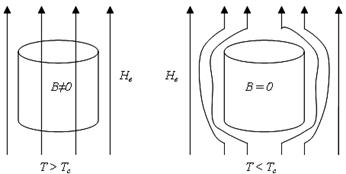
В 1933 г. В.Мейсснер и Р.Оксенфельд изучали распределение магнитного потока вокруг оловянных и свинцовых образцов, охлажденных в магнитном поле. Они обнаружили, что при Т < Т_С образцы, кроме сверхпроводимости, приобретают свойства идеального диамагнетика, т.е. полностью выталкивают магнитное поле (рис. 5.9).

а) б)

Рис. 5.9. Выталкивание магнитного поля из сверхпроводника

Исчезновение магнитного поля внутри сверхпроводника связано с появлением на его поверхности экранирующих токов, которые создают внутри образца магнитное поле, равное по величине и противоположное по знаку внешнему полю. В области протекания этих токов магнитное поле спадает от величины Н_е на поверхности образца до нуля – на глубине λ. Величина λ называется глубиной проникновения и для НТСП составляет 10…100 нм.

Выталкивание магнитного поля наблюдается только в слабых полях. Если же напряженность поля достигает критической величины, то сверхпроводящее состояние разрушается и образец переходит в нормальное состояние. При повышении температуры в области 0 <Т<Т_С величина критического поля уменьшается

Н_С (Т) = Н_С ₀[ 1 -(Т / Т_С) ² ]. (5.66)

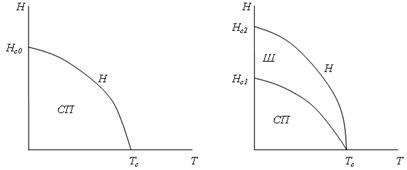
Зависимость (5.66) графически изображена на рис. 5.10, а.

а) б)

Рис. 5.10. Зависимость критического магнитного поля от температуры:

а – сверхпроводник 1-го рода; б – сверхпроводник 2-го рода;

Ш – состояние Шубникова; Н – нормальное состояние

На графике видно, что сверхпроводник можно перевести в нормальное состояние, увеличив либо температуру, либо магнитное поле. Таким образом, оба этих фактора являются дестабилизирующими.

Анализируя эффект Мейсснера, следует отметить, что сверхпроводимость разрушается не только под действием внешнего магнитного поля (наведенного тока), но и при протекании транспортного тока, плотность которого больше критической j_c

j_c = bH_c / λ, (5.67)

где b – константа системы измерений.

Данное явление называют эффектом Силсби.

Таким образом, существуют критические параметры, превышение которых совместно или поодиночке приводит к разрушению сверхпроводимости: критическая температура Т_С, критическое магнитное поле В_С и критическая плотность тока j_C.

Рассмотренные ранее сверхпроводники относятся к 1-му роду СП. Для них характерен переход из сверхпроводящего в нормальное состояние одновременно всего объекта.

Сверхпроводники 2-го рода имеют 2 критических поля: Н_С1 (Т) и Н_С2 (Т) (рис. 5.10, б). При поле, меньшем нижнего критического значения, магнитный поток не проникает в образец и тот ведет себя как СП 1-го рода. Если магнитное поле превышает верхний предел Н_С2, весь образец находится в нормальном состоянии. При Н_С1 < Н < Н_С2 происходит частичное проникновение магнитного потока в образец и возникает смешанное состояние, или состояние Шубникова. Магнитный поток проникает в образец в виде тонких вихревых нитей, так называемых вихрей Абрикосова. В центре вихря содержится нормальная область, окруженная экранирующими токами. Вихри Абрикосова могут служить носителями информации в криомикроэлектронике, они могут целенаправленно передвигаться, зарождаться, аннигилировать.

Необходимо отметить, что все высокотемпературные сверхпроводники относятся к СП 2-го рода.

5.7. Основы теории Бардина – Купера – Шриффера

После открытия сверхпроводимости было предпринято множество попыток объяснить столь необычные эффекты сверхпроводимости. Среди этих работ многие теории до сих пор сохранили свое значение. Так, в 1935 г. Ф. и Г. Лондоны, используя двухжидкостную модель, получили так называемые уравнения Лондонов, объясняющие многие макроскопические свойства сверхпроводников.

В 1950 г. В.Л. Гинзбург и Л.Д. Ландау построили теорию сверхпроводимости, основанную на квантовой механике. Решением уравнений Гинзбурга – Ландау были объяснены и предсказаны многие свойства сверхпроводников, в том числе идеальный диамагнетизм, квантование магнитного потока и ряд других.

Несмотря на то, что теория Гинзбурга – Ландау, получившая дальнейшее развитие в работах А. А. Абрикосова и Л. П. Горькова, описывала многие свойства сверхпроводников, оно не могла объяснить явления сверхпроводимости на микроскопическом уровне.

Ответы на большинство вопросов дала теория, опубликованная Дж. Бардиным, Л. Купером и Дж. Шриффером в 1957 г. – теория БКШ, раскрывшая микроскопический механизм сверхпроводимости. Исходным пунктом этой теории является представление о притяжении между электронами, находящимися вблизи уровня Ферми. Такое притяжение электронов возможно за счет их обмена фононами кристаллической решетки.

Купер показал, что при наличии между электронами притяжения, даже сколь угодно малого, нормальное состояние многоэлектронной системы становится неустойчивым из-за процесса спаривания. Электроны с противоположными импульсами и антипараллельными спинами объединяются в куперовские пары, обладающие меньшей энергией, чем отдельные нормальные электроны.

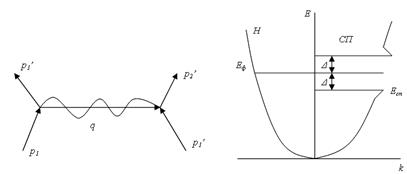
Рассмотрим, как осуществляется притяжение между электронами – одноименно заряженными частицами. Кристаллическая решетка состоит из положительных ионов, которые притягивают электроны. Но и электроны притягивают ионы, смещая их от положения равновесия. Это смещение незначительно вследствие огромной разности масс иона и электрона, но оно существует: как говорят, решетка поляризуется. Такое смещение зарядов нарушает однородность поля ионов и может быть интерпретировано как появление положительного заряда. Этот виртуальный заряд притягивает другой электрон, находящийся поблизости. Область поляризации решетки не является неподвижной, она перемещается вместе с электроном, который ее формирует. Если такое притяжение будет преобладать над кулоновским отталкиванием, то электроны образуют пары. Взаимодействие электронов через решетку можно представить как результат испускания фонона одним электроном и поглощения другим (рис. 5.11, а).

p₂

а) б)

Рис. 5.11. Образование куперовских пар: а – испускание и поглощение электронами

фонона; б – спектр сверхпроводника

Пусть Т = 0К и фононы решетки в кристалле отсутствуют. Первый электрон с импульсом 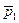испускает фонон q, который поглощается вторым электроном . Электроны после взаимодействия изменяют импульсы на 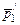и . При этом выполняется закон сохранения импульсов

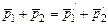(5.68)

или, соответственно, для волновых векторов

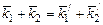, (5.69)

где 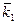, 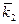– волновые векторы электронов до взаимодействия;

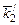, – векторы после взаимодействия.

Фонон q, о котором идет речь – необычный, виртуальный фонон. В отличие от обычного, он не перемещается свободно по решетке, а только от одного электрона к другому. Как мы уже отмечали, при нулевой температуре обычных фононов в решетке нет.

Поскольку куперовская пара содержит электроны с антипараллельными спинами, она имеет нулевой спин и является бозоном. Согласно распределению Бозе – Эйнштейна все пары занимают уровень Е_Ф – Δ (рис. 5.11, б). На рисунке для сравнения показаны энергетические спектры нормальной (левая часть) и сверхпроводящей фаз. Как можно видеть в СП-состоянии энергетический спектр имеет щель шириной, равной энергии связи пары 2Δ. При Т ≈ 0 ширина энергетической щели максимальна и равна

2 Δ (0) = 3,5 kТ_С, (5.70)

где k – постоянная Больцмана.

Существование энергетической щели получило экспериментальное подтверждение, в частности, при исследовании спектра поглощения сверхпроводника в дальней ИК области. При частоте, для которой hν = 2 Δ, начинается интенсивное поглощение излучения. Энергия 2Δ затрачивается на разрыв пары. При повышении температуры также возможны переход электронов через щель и образование над ней неспаренных электронов. Величина щели при этом уменьшается и при Т = Т_С щель исчезает.

Вблизи Т_С энергетическая щель изменяется с изменением температуры, согласно выражению

Δ (Т) = 1,74Δ(0)(1-Т / Т_С)^1/2. (5.71)

Оценим размеры куперовской пары ξ ₀ и их долю n_S в общем числе электронов. Для типичных значений СП: Е_Ф = 10 эВ, к_Ф = 10⁸ см^-1 и Т_С = =10К получаем ξ ≈ 10^-4 см. Это означает, что электроны в паре разнесены на 10³…10⁴ периодов кристаллической решетки.

Концентрацию куперовских пар при Т = 0К можно определить интегрированием выражения (5.70). Она составляет 10^-4 от общей концентрации свободных электронов. При повышении температуры эта концентрация убывает и при Т = Т_С n_S = 0.

Как уже отмечалось, в отличие от отдельных электронов – фермионов, куперовские пары являются бозонами. Для них не существует постулата запрета Паули, т.е. куперовские пары находятся в одном состоянии и соответствуют друг другу по всем физическим параметрам. Волновые функции СП электронов являются когерентными, т.е. их фазы отличаются друг от друга на постоянную величину. Таким образом, куперовские пары (“бозе-конденсат”) представляют собой взаимосвязанный ансамбль.

В электрическом поле куперовские пары будут ускоряться, т.е. получать результирующий импульс из-за взаимосвязи между парами. Этот импульс должен быть абсолютно одинаковым для всех пар. Однако пара не может обмениваться энергией с решеткой, иначе она перейдет в другое энергетическое состояние, что запрещено условиями модели. Образно говоря, ансамбль принимает на себя это взаимодействиие, и, пока оно не велико, полный импульс ансамбля сохраняется, т.е. электрический ток не изменяется. Это означает, что перенос заряда через решетку осуществляется без сопротивления.

Если энергия воздействия становится больше, чем энергия связи (Т > Т_С, j > j_C, В > В_С), тогда связь пары разрушится и она покидает квантовый бозе-конденсат.

Теория БКШ обосновала многие эмпирические соотношения в сверхпроводимости.

Выше мы рассматривали свойства обычных низкотемпературных сверхпроводников (см. табл. 5.1). Здесь необходимо сказать об основных отличиях, которые имеют ВТСП.

1. Высокое значение температуры перехода лежит в области азотных температур (Т > 77К), что не объясняется существующей теорией БКШ.

2. Химические связи ВТСП. В отличие от НТСП, которые обладают металлической (металлы, сплавы) или ковалентной химической связью (полупроводники), ВТСП представляют собой оксиды. Характер связи приводит к тому, что в таких сверхпроводниках концентрация носителей меньше.

3. Нормальное удельное сопротивление (Т > Т_С) ВТСП соединений значительно больше, чем у обычных металлов, и сильно зависит от содержания кислорода.

4. В отличие от обычных НТСП, где температурный переход занимает максимум 1…2К, в ВТСП этот переход более 4К и зависит от способа приготовления образца

5. Длина когерентности Гинзбурга-Ландау в НТСП составляет
10^-6 м. Для ВТСП эта величина гораздо меньше – 0,5 … 30А º. Напомним, что длина когерентности характеризует расстояния, на которых изменяется плотность сверхпроводящих пар. Такое малое значение длины когерентности в ВТСП приводит к необычным явлениям. В частности, двумерные (поверхностные) дефекты в ВТСП могут образовывать джозефсоновские барьеры.

Эти и другие замечания позволяют сделать вывод о том, что процессы в ВТСП подобны традиционным, однако существуют отличия, связанные, в основном, с малой длиной когерентности, большой глубиной проникновения магнитного поля и т.д., которые необходимо учитывать при проектировании приборов ВТСП микроэлектроники. Некоторые возможные приложения эффектов сверхпроводимости в криомикроэлектронике будут рассмотрены ниже (п. 10.2).

Эффекты Джозефсона

В 1962 г. Б. Джозефсон в результате вычислений пришел к выводу, что туннельный ток куперских пар I_S в структуре СДС не только возможен, но и сопоставим по величине с одночастичным током. Максимальное значение I_S можно определить из выражения

I_m = πΔ /(2eR_N), (5.72)

где R_N – сопротивление туннельного контакта в нормальном состоянии.

Из вычислений Джозефсона следовало, что постоянный ток I_S – должен протекать в отсутствие разности потенциалов на контакте, причем этот ток определяется разностью фаз волновых функций сверхпроводящих конденсатов в одном и другом сверхпроводниках. Джозефсон предсказал и другие свойства структуры, которые впоследствии были обнаружены экспериментально.

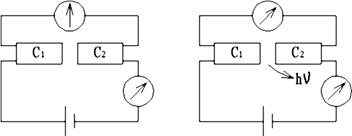
Рассмотрим процессы, протекающие в структуре СДС, если диэлектрический зазор составляет порядка 1 нм (рис. 5.12, а).

а) б)

Рис. 5.12. Эффект Джозефсона: а – стационарный; б – нестационарный

Если подать на СДС структуру разность потенциалов, через нее потечет ток, падение напряжения на структуре и сопротивление будут равны нулю. Структура ведет себя, как сплошной сверхпроводящий образец. Ток протекает и по диэлектрическому зазору беспрепятственно. Это явление получило название стационарного эффекта Джозефсона. При увеличении тока наступает такой момент, когда на структуре возникнет постоянная разность потенциалов и одновременно из зазора пойдет электромагнитное излучение высокой частоты (см. рис. 5.12, б). Очевидно, что кроме постоянного появляется переменный ток высокой частоты. Это явление называют нестационарным эффектом Джозефсона. Напомним, что волновая функция куперовской пары является суперпозицией состояний с противоположными k, близкими по значению к k_Ф. Волновые функции пар совпадают, поскольку пары являются бозонами. Таким образом, все куперовские пары находятся в одном квантовом состоянии и описываются одной функцией. Изменение концентрации влияет только на амплитуду волновой функции. Волновая функция куперовских пар может быть определена так:

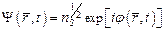, (5.73)

где 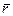– радиус-вектор;

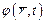– фаза;

n_S – концентрация куперовских пар.

Поскольку движение всех пар строго коррелировано и центры масс всех пар движутся с одинаковым импульсом, то общий импульс электронной сверхпроводящей системы равен Р

P = n_Sħk. (5.74)

Фаза функции (5.73) определяется следующим образом:

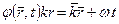. (5.75)

Волновые функции сверхпроводящих электронов проникают в зазор вследствие туннелирования и определяют функцию в промежуточном слое

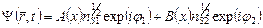, (5.76)

где А (х) и В (х) определяют глубину проникновения волновых функций в зазор.

При х = 0 A (0) = 1и с ростом х быстро уменьшается до нуля; аналогично при x = d (d – толщина зазора) B(d) = 1и при x<d быстро уменьшается до нуля. Плотность вероятности волновой функции (5.76) определяется по известной формуле и может быть записана так:

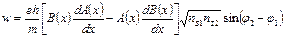. (5.77)

Из (5.77) может быть получено выражение для плотности тока туннелирования куперовских пар

j_S = j_m sin(φ₂ – φ₁) = j_m sin θ, (5.78)

где θ – разность фаз волновых функций пар по обе стороны барьера.

Уравнение (5.78) иногда называют уравнением Джозефсона. Другое важное уравнение Джозефсона связывает напряжение на барьере со скоростью изменения разности фаз

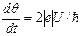. (5.79)

Используя выражения (5.78) и (5.79), можно найти мощность (Ujs)
а затем, с помощью интегрирования по времени, найти энергию контакта

Е (θ) = -(ħI_m / 2 | e |)cos θ. (5.80)

Вольт-амперная характеристика (ВАХ) перехода Джозефсона объединяет оба эффекта (рис. 5.13).

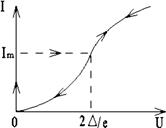
Рис. 5.13. ВАХ переходов Джозефсона (стрелками показано направление тока)

На начальном участке графика (0 – I_m) ток I_S через переход растет, а падение напряжения остается равным нулю. Этот участок соответствует стационарному эффекту, здесь происходит туннелирование пар через потенциальный барьер. Поскольку падения напряжения нет, нет и сдвига в энергетической диаграмме (рис. 5.14, а), уровни Е_СП в одном и другом сверхпроводнике находятся на одной высоте – между ними возможны туннельные переходы.

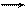
а) б)

Рис. 5.14. Энергетическая диаграмма перехода Джозефсона: а – стационарный эффект;

б – нестационарный эффект

При увеличении тока через переход (I_S = I_m) наступает такое состояние, что становится возможным одночастичное туннелирование (рис. 5.14, б). Система переходит скачком в это состояние и приобретает падение напряжения

U_m = 2Δ/ е. (5.81)

В связи с изменением энергетической диаграммы сохранение энергии пары до и после перехода нарушается, поскольку энергия пары в зависимости от направления перехода либо возрастает, либо убывает. В отсутствие фононов такой энергии (Т<Т_С) разница энергии пары либо поглощается, либо выделяется в виде кванта электромагнитного излучения с частотой

ω = 2 eU / ħ. (5.82)

Туннельный ток куперовских пар из постоянного (стационарный эффект) становится переменным, величина которого равна

I = I_msin [(2 eU / ħ) t ]. (5.83)

Если U = 1 мВ, то частота составит 485 ГГц, что соответствует длине волны λ ≈ 0,6 мм. Таким образом, переход Джозефсона может служить в качестве генератора СВЧ колебаний с возможностью перестройки частоты.

Далее на ВАХ возрастают и ток, и напряжение, однако обратный ход характеристики не совпадает с прямым, т.е. имеет место гистерезис при Т > 0, связанный с существованием нормальных электронов.

Необычные результаты дает наложение на переход Джозефсона магнитного поля параллельно плоскости контакта. Поле сильно изменяет плотность туннельного тока через переход, проникая в зазор. В этом случае сверхпроводящий ток I_S становится функцией магнитного потока Ф_К или, точнее, функцией отношения Ф_К / Ф ₀

Ф_К / Ф ₀ = 2λlB / Ф ₀, (5.84)

где l – длина контакта;

λ – глубина проникновения поля в сверхпроводник;

В – индукция внешнего поля;

Ф ₀= h/2е – квант магнитного потока.

Величина туннельного тока через переход определяется выражением

I_S = I_m (Ф_К)sin φ, (5.85)

где. (5.86)

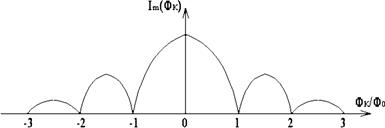
Рис. 5.15. Зависимость критического тока перехода Джозефсона

от изменения внешнего магнитного поля

Из (5.86) следует, что критический ток перехода Джозефсона осциллирует при изменении внешнего поля, обращаясь в нуль всякий раз, когда отношение (5.84) становится целой величиной (рис. 5.15). Зависимость I_m (Ф_К) позволяет измерять магнитное поле с высокой точностью, поскольку Ф ₀ очень мало. Условие обращения в нуль функции I_m (Ф_к) имеет интересную физическую интерпретацию. Оказывается, на переходе образуются магнитные вихри, похожие на вихри Абрикосова. Разница состоит в том, что эти вихри не содержат нормальной фазы в центре, их ось расходится в диэлектрическом зазоре (рис. 5.16). Такие магнитные вихри можно использовать в качестве динамических неоднородностей для обработки информации, так же, как вихри Абрикосова.

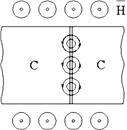
Рис. 5.16. Магнитные вихри на переходе Джозефсона

В заключение отметим, что эффекты Джозефсона возникают не только в описанной СДС структуре, но и в других структурах, объединяемых общим понятием "слабосвязанные сверхпроводники".

На рис. 5.17 показаны примеры таких структур, используемых в криоэлектронике.

б)

в)

г)

а)

д)

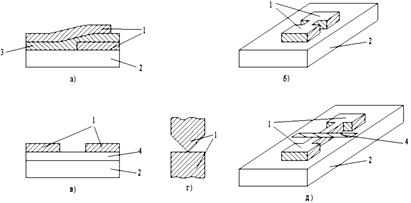
Рис. 5.17. Основные виды слабосвязанных сверхпроводящих структур:

а – туннельный переход; б – мостик с микросужением; в – мостик переменной толщины;

г – точечный контакт; д – мостик, созданный на эффекте близости. 1 – сверхпроводящие электроды; 2 – подложка; 3 – изолирующий слой; 4 – пленка мостика

Различные типы слабосвязанных структур имеют разные параметры (табл. 5.2). Например, структура “мостик” не имеет гистерезиса, что выгодно отличает ее от структуры СДС.

Таблица 5.2

Параметры слабосвязанных сверхпроводниковых структур, изготовленных

методами интегральной технологии

Материал элемента слабой связи	Структура	d, нм	R_N, Ом	U_m, мВ	С, пФ
диэлектрик	“сэндвич”	1 – 2
полупроводник	- v -	5 – 50	0,1 – 10		0,1
металл	- v -	10²	10^-6	10^-3	10^-2
полуметалл	“мостик”	10²	0,1 – 1	0,1	10^-2
металл	- v -	10²	0,1	0,1	10^-2
вырожденный полупроводник	“планарная”	10 – 10²			10^-2
узкозонный полупроводник	- v -	10²		0,5	10^-3

Джозефсоновские переходы находят самое широкое распространение как в аналоговой, так и в цифровой криоэлектронике.

Контрольные вопросы и задания

1.1. Дайте определение подвижности носителей заряда.

1.2. Сформулируйте закон Ома.

1.3. Какие силы действуют на электрон в твердом теле?

1.4. Запишите основное уравнение динамики для электрона.

1.5. Что определяет время релаксации электрона?

1.6. Определите подвижность электрона в металле при Т = 300К, если λ =10 нм.

1.7. Определите подвижность электрона в кремнии при Т = 300К.

1.8. Определите удельную электропроводность германия при Т = 300К.

2.1. Назовите факторы, ограничивающие подвижность носителей в твердом теле.

2.2. Как влияет температура на подвижность вырожденных полупроводников?

2.3. Как влияет температура на подвижность металлов?

2.4. Как влияет температура на подвижность слаболегированных полупроводников?

2.5. Дайте определение электрон-фононного рассеяния.

2.6. Дайте определение электрон-ионного рассеяния.

3.1. Какие факторы влияют на концентрацию носителей в чистом полупроводнике?

3.2. Какие факторы влияют на уровень Ферми в чистых полупроводниках?

3.3. Удельное сопротивление собственного германия при Т = 300К составляет 0,45Ом∙м. Подвижности электронов и дырок соответственно 0,39 и 0,19 м²/(В∙с). Определите собственную концентрацию электронов и дырок.

3.4. Найдите положение уровня Ферми при Т = 300К для собственного германия.

3.5. На сколько градусов нужно повысить температуру в чистом германии от начальной (300К), чтобы концентрация носителей возросла вдвое.

3.6. Что называют зоной истощения примеси?

3.7. Найдите положение уровня Ферми при Т = 300К для кристалла германия, содержащего 5∙10¹⁶см^-3 атомов мышьяка.

3.8. Определите концентрацию примеси мышьяка для удвоения концентрации носителей при Т = 300К.

3.9. Запишите условие действующих масс.

3.10. Когда и где формируются примесные зоны?

4.1. Какие факторы влияют на проводимость собственных полупроводников?

4.2. Дайте определение ширины запрещенной зоны.

4.3. Как можно определить ширину запрещенной зоны7

4.4. Удельное сопротивление собственного гермния при Т = 300К составляет 0,43 Ом·м. Какими путями можно вдвое уменьшить его?

4.5. Определите удельную электропроводность кремния при Т = 300К, если N_a = 2,3∙10¹⁹м^-3, N_д = 2,2∙10 ¹⁹ м^-3.

4.6. Образец кремния p -типа длиной 5 м, шириной 2 мм, толщиной 1 мм имеет сопротивление 100 Ом. Определите концентрацию примеси, если n_i = 2,5∙10 ¹⁶м^-3, μ_n = 0,12 м²/(В∙с), μ_p = = 0,025 м²/(В∙с).

4.7. Определите отношение электронной проводимости к дырочной для предыдущей задачи.

4.8. Объясните поведение графиков на рис. 5.7, б.

4.9. Определите величину σ ₀ для задачи 4.4.

5.1. Чем определяется электропроводность металлов?

5.2. Какие факторы определяют электропроводность металлов при низких температурах?

5.3. Поясните смысл графика на рис. 5.7, а.

5.4. Какие факторы определяют проводимость бинарных сплавов?

5.5. Что вызывает отклонение графика рис. 5.7, б?

6.1. В чем заключается эффект сверхпроводимости?

6.2. Какова природа сверхпроводящего состояния?

6.3. Опишите эффект Мейсснера.

6.4. Как проникает магнитное поле в сверхпроводнике?

6.5. Каков смысл критического поля?

6.6. Каков смысл критического тока?

6.7. Опишите отличие сверхпроводников второго рода.

6.8. Дайте понятие куперовской пары.

6.9. Назовите основные положения теории БКШ.

6.10. Что такое ВТСП?

6.11. Назовите основные особенности ВТСП?

6.12. Какова природа энергетической щели в СП?

7.1. Какие типы тунеллирования возможны при низких температурах?

7.2. Опишите и объясните стационарный эффект Джозефсона.

7.3. Опишите и объясните нестационарный эффект Джозефсона.

7.4. Какова природа излучения Джозефсона?

7.5. Приведите ВАХ джозефсоновского перехода.

7.6. Как влияет магнитное поле на эффект Джозефсона?

7.7. Опишите возможные варианты джозефсоновского контакта.

Глава 6
РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ НОСИТЕЛИ ЗАРЯДА

Образование свободных электронов в полупроводниках связано с переходом их в зону проводимости из валентной зоны или с примесных уровней. Свободные дырки образуются в валентной зоне в результате ухода электронов в зону проводимости или на примесные уровни. Эти процессы называют генерацией носителей заряда, они связаны с поглощением энергии электронами. В обычных условиях эта энергия сообщается электрону при взаимовоздействии его с решеткой и имеет тепловую природу. Одновременно с процессом генерации происходит процесс рекомбинации. Электроны вновь возвращаются в валентную зону или на донорные уровни, что приводит к снижению концентрации свободных носителей заряда. При рекомбинации носителей кристаллической решетке передается энергия, затраченная на их генерацию. Динамическое равновесие между процессами генерации и рекомбинации при любой температуре приводит к установлению равновесной концентрации носителей, описанной в п.5.3. В этом случае носители находятся в энергетическом равновесии с кристаллической решеткой и называются равновесными носителями.

Помимо теплового возбуждения возможны и другие способы генерации носителей в полупроводниках: под действием света, сильного электрического поля, ионизирующего излучения, инжекции через контакт и др. Такие носители имеют избыточную концентрацию по сравнению с равновесными носителями и энергию, отличную от энергии равновесных носителей. Они называются неравновесными.