Электронно-дырочный переход. Контакт двух полупроводников с разным типом проводимости получил название электронно-дырочного перехода

 

Контакт двух полупроводников с разным типом проводимости получил название электронно-дырочного перехода, или p-n – перехода. Он исключительно широко используется для создания дискретных активных элементов: диодов, транзисторов и т.д. Еще более широко они применяются в микроэлектронике для создания активных и пассивных элементов интегральных схем.

Технология изготовления p-n-переходов разработана достаточно хорошо, а их свойства глубоко исследованы как теоретически, так и экспериментально. Создать p-n переходы можно различными путями. Наибольшее практическое применение нашли способы вплавления, диффузии, эпитаксиального наращивания, ионной имплантации и др. [19]. Эти способы позволяют создавать самые разнообразные по своей структуре переходы.

По характеру распределения примесей можно выделить резкие и плавные, симметричные и несимметричные p-n – переходы. В резких переходах концентрация доноров и акцепторов скачкообразно изменяется на границе p и n областей. Плавные переходы имеют конечный градиент концентрации примесей, изменяющихся в широком диапазоне. В симметричных переходах концентрация примесей и концентрация основных носителей в обеих областях одинаковы. Наибольшее распространение получили сильно несимметричные переходы, где p_p >> n_n или p_p << n_n.

В этом разделе мы рассмотрим важнейшие выводы теории применительно к равновесному состоянию p-n-перехода.

 

Рис. 7.7. Равновесное состояние p-n перехода: а – распределение примесей; б – зонная диаграмма; в – распределение носителей; д – распределение объемного заряда

 

Пусть два образца с различным типом проводимости приведены в контакт. Необходимо напомнить, что этот эксперимент является идеализированным, поскольку в нем игнорируются реальные свойства поверхностей образцов.

д)

Очевидно, что работа выхода электронов в n-полупроводнике меньше, чем в p-полупроводнике, поэтому возникают поток электронов из n-области в p-область и аналогичный поток дырок в n-область – диффузионный ток. Границу раздела p- и n-областей называют металлургической границей полупроводников. Переход носителей через металлургическую границу приводит к образованию около нее обедненных областей: положительного заряда в n-области и отрицательного в p-области (рис. 7.7, г) Эти заряды образованны ионами соответственно донорной и акцепторной примеси.

Процесс переноса носителей заряда прекратится тогда, когда уровни Ферми выровняются. Ток, создаваемый электрическим полем объемного заряда, (дрейфовый ток) полностью компенсируется диффузионным током, обусловленным градиентом концентрации примеси. На рис. 7.7 приведены графики для равновесного p-n перехода. Найдем зависимость для параметров p-n перехода. При этом будем считать, что полупроводники, образующие переход, не вырождены, а температура такова, что все атомы примеси уже ионизированы.

Высота потенциальных барьеров для электронов φ _{0 n} и дырок φ _{0 p} одинакова и равна разности уровней Ферми (или работ выхода)

, (7.19)

Подставляя в это уравнение выражения (5.45) и (5.50), с учетом закона действующих масс получим

(7.20)

Чтобы найти распределение потенциала и напряженности поля в областях объемного заряда, необходимо решить уравнение Пуассона (7.5). Для упрощения процедуры предположим, что справа от металлургической границы, в областях 0 <x<d_p, объемный заряд равен ep_p, а слева на участке -d_n<x< 0, его величина равна en_n. При этом для х ≤ -d_n, φ = 0, а для x = d_p, φ = φ ₀.

Решение уравнения Пуассона дает выражение для потенциала φ инапряженности электрического поля E

в области d_n < х< 0

, (7.21)

, (7.22)

а в области 0< х< d_n

, (7.23)

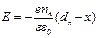. (7.24)

Поскольку рассматриваемые функции являются непрерывными на металлургической границе, они должны принимать одно значение при , . Используя эти условия легко найти выражение для полной толщины объемного слоя и ее составляющих

, (7.25)

, . (7.26)

Из последних выражений видно, что толщина слоя объемного заряда тем больше, чем меньше в ней концентрация основных носителей.

Если p-n-переход является существенно несимметричным, то полная толщина слоя объемного заряда практически равна толщине слоя в той области полупроводника, где концентрация основных носителей меньше. Например, для случая n_n << p_p, практически весь слой объемного заряда лежит в p-области и

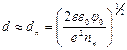. (7.27)

Так, для германия при p_p =10²³ м^-3 и п_n =10²¹ м^-3, d_р ≈8·10^-9 м, а d_п = 7,7·10^-7 м, т.е. .

Приведенные рассуждения относятся к резкому переходу, в котором концентрация примесей меняется практически скачкообразно (рис. 7.7, а). В случае тянутых и диффузионных переходов изменение конструкции в переходе происходит плавно. Принимая для этого случая линейную функцию N (x)= ax и решая уравнение Пуассона, получим следующее выражение для толщины слоя объемного заряда:

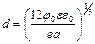. (7.28)

Параметр a называют градиентом концентрации примеси.