Проводимость и подвижность носителей

 

В отсутствие внешнего электрического поля электронный газ в твердом теле находится в равновесном состоянии и описывается равновесными функциями распределения Ферми-Дирака (вырожденное состояние) или Максвелла-Больцмана (невырожденное состояние). На рис. 5.1, а, б приведены графики распределения f_Ф (υ_x) и f_M (υ_x). Они симметричны относительно оси ординат, что говорит об одинаковой плотности заполнения состояний, отличающихся направлением скорости υ_х. По этой причине и алгебраическая средняя скорость движения электронов равна нулю. Такая картина вполне естественна в случае теплового движения.

 

а) б)

Рис. 5.1. Графики функций распределения Ферми-Дирака (а)

и Максвелла-Больцмана (б): 1 – Е =0; 2 – Е ≠0

Равновесие в электронном газе устанавливается в результате взаимодействия электронов с кристаллической решеткой. Электроны взаимодействуют как с колебаниями решетки – электрон-фононное рассеяние, так и с дефектами твердого тела, например, электрон-ионное рассеяние. Такой обмен энергиями приводит к установлению энергетического равновесия между электронным газом и кристаллической решеткой. В этом случае электроны называют равновесными.

Если к кристаллу приложить внешнее электрическое поле напряженности Е, то в нем возникнет смещение функций распределения (рис. 5.1, а, б) и появится электрический ток, плотность которого i, пропорциональна Е

i = σЕ, (5.1)

где σ – удельная электропроводность проводника.

У хороших проводников, таких, например, как металлы, электропроводность достигает величины 10⁷…10⁸ Ом^-1м^-1, у хороших изоляторов – 10^-12…10^-14 Ом^-1м^-1.

Обратная σ величина ρ называется удельным сопротивлением проводника

 

ρ =1/ σ. (5.2)

Возникновение тока в проводнике говорит о том, что под действием электрического поля электроны совершают направленное движение, характеризуемое дрейфовой скоростью – J_д. Сила, действующая на электрон со стороны внешнего поля F_е, пропорциональна величине Е и заряду электрона е. Поскольку заряд электрона отрицателен, F_е и Е противоположно направлены

 

F_е = - еЕ. (5.3)

Как мы уже говорили, электрон взаимодействует с кристаллической решеткой, и на него действует сила сопротивления, пропорциональная его массе m_n^* и дрейфовой скорости. Поскольку сила сопротивления F_с направлена против движения электрона, можно записать основное уравнение динамики в следующем виде:

, (5.4)

где 1/ τ – коэффициент пропорциональности, входящий в выражение для силы сопротивления.

Из выражения (5.4) видно, что после включения поля дрейфовая скорость электрона будет возрастать, пока сила сопротивления не окажется равной силе электрического поля. Когда эти силы сравняются, ускорение электрона будет равно нулю.

Выражение (5.4) примет вид

, (5.5)

или

. (5.6)

Отношение дрейфовой скорости электрона к напряженности поля называют его подвижностью μ_n

J_д = μ_nЕ. (5.7)

 

Для электронов μ_n < 0, для дырок μ_p > 0.

Выясним теперь физический смысл введенного в (5.4) коэффициента τ. Для этого рассмотрим картину в проводнике при выключении электрического поля, E =0. Выражение (5.4) примет вид

. (5.8)

Дифференциальное уравнение (5.8) имеет решение

 

J_д (t)= J_{д 0}exp(- t / τ), (5.9)

где J_{д 0} – дрейфовая скорость электрона сразу после выключения поля при t = 0.

 

Последние уравнения описывают процесс релаксации – самопроизвольное возвращение системы в положение равновесия. Время релаксации – τ характеризует время уменьшения возбуждения в е раз. В нашем случае возбуждением системы является смещение функции распределения и придание электронному газу дополнительной энергии дрейфового движения.

Движение электронов в кристалле удобно описывать, используя понятие длины их свободного пробега λ. По аналогии с кинетической теорией газов можно считать, что электрон движется в кристалле прямолинейно до тех пор, пока не встретится с дефектом или фононом решетки и не рассеется на нем. Этот средний отрезок, который проходит электрон между двумя актами рассеяния и называют длиной свободного пробега.

Если электрон в единичном акте рассеяния теряет всю избыточную энергию дрейфового движения, то для процесса релаксации можно записать простое соотношение

 

λ = J_Тτ, (5.10)

где J_Т – тепловая скорость электрона.

 

Часто, однако, для полной потери энергии электрону требуется не одно, а несколько актов рассеяния – ν. Очевидно, что путь, который электрон пройдет при этом, будет в ν раз больше и время релаксации также возрастет

. (5.11)

Подставив последнее выражение в (5.6), получим соотношение, которое связывает подвижность носителей заряда с их параметрами

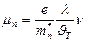. (5.12)

Теперь вернемся к выражению (5.1) и уточним физический смысл понятия удельной проводимости. Для этого мысленно выделим в проводнике параллелепипед, ребра которого параллельны линиям тока и равны величине J_д, а площадь поперечного сечения равна единице. Пусть все электроны объема в единицу времени пройдут через поперечное сечение. Их заряд можно выразить как

 

Q = Ven = J_дen, (5.13)

где V – объем параллелепипеда;

n – концентрация электронов.

Одновременно выражение (5.13) имеет смысл плотности тока i. Сравнивая (5.13) и (5.1), можно записать

i = enJ_д = enμЕ, (5.14)

 

т.е. σ = enμ, (5.15)

или с учетом выражения (5.12)

. (5.16)

Выражения (5.11) и (5.14) позволяют определить значения подвижности и электропроводности электронного газа. Однако в начале раздела мы привели два возможных варианта: вырожденный и невырожденный газ. Теперь попытаемся установить, как влияет состояние электронного газа на его свойства.

В случае невырожденного газа электроны практически не встречаются друг с другом и их поведение не ограничивается постулатом Паули. Все электроны проводимости невырожденного газа принимают независимое друг от друга участие в создании электрического тока. Тогда формулы (5.12) и (5.16) должны содержать средние параметры газа

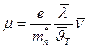, (5.17)

. (5.18)

Другая картина наблюдается в случае вырожденного газа. На рис. 5.1, б видно, что в этом случае все состояния в интервале – υ_Ф....υ_Ф заняты электронами. Поэтому внешнее поле может воздействовать только на электроны, расположенные близ уровня Ферми, переводя их из левой области распределения в правую, как показано стрелками на рис. 5.1, а. Для выражений (5.12) и (5.16) в случае вырожденного газа необходимо использовать параметры λ _Ф. υ_ТФ, τ_Ф, ν_Ф

, (5.19)

. (5.20)