В полупроводниках
Итак, концентрация носителей в собственных и примесных полупроводниках сильно зависит от температуры. Одним из основных параметров, характеризующих газ свободных носителей в полупроводниках, является уровень Ферми, который также зависит от температуры.
В собственных и слаболегированных полупроводниках, в отличие от металлов, электронный газ является невырожденным и может быть описан классической статистикой Максвелла-Больцмана.
При температуре Т (Т >0 К) в зоне проводимости такого полупроводника находятся электроны, а в валентной зоне – дырки. Обозначим их концентрации соответственно n и p. Примем за начало отсчета энергии электронов дно зоны проводимости. Используя ранее полученные соотношения (п.3.3) для функции Максвелла-Больцмана, можно определить число частиц в интервале Е, E+dE как
. (5.33)
В невырожденных полупроводниках ЕФ является величиной отрицательной и, по определению, находится ниже дна зоны проводимости (рис. 5.3, а).
Обозначим расстояние от потолка валентной зоны до уровня Ферми как μ ', а расстояние от уровня Ферми до дна валентной зоны – μ (рис. 5.3, а).
Из рисунка очевидно следует, что
ЕФ+μ ' =Еg, μ ' =- (Еg-μ), (5.34)
где Еg – ширина запрещенной зоны полупроводника.
|
|
а) б)
Рис. 5.3. Зонная структура полупроводника: а – температурная постоянная;
б – температурная зависимость уровня Ферми; 1 – mp* = mn*; 2 – mp* > mn*; 3 – mp* < mn*
Полное число электронов, находящихся в зоне проводимости, можно определить, интегрируя (5.33) в интервале от 0 до Е2. Поскольку функция exp (- E / kT) спадает очень быстро, то верхний предел интегрирования Е2 (здесь не отрицательный) можно заменить приближенно на бесконечность так, что
. (5.35)
Вычисление этого интеграла приводит к следующему результату:
, (5.36)
где NC – эффективная плотность состояний в зоне проводимости.
Подобный расчет, проведенный для плотности дырок в валентной зоне, приводит к выражению
, (5.37)
где NV – эффективная плотность состояний в валентной зоне.
Из (5.36) и (5.37) следует, что концентрация свободных носителей заряда в данной зоне определяется расстоянием этой зоны от уровня Ферми: чем больше это расстояние, тем ниже концентрация носителей.
В собственных полупроводниках концентрация электронов в зоне проводимости ni равна концентрации дырок в валентной зоне
ni = pi. (5.38)
Приравнивая правые части (5.36) и (5.37) и решая полученное уравнение относительно ЕФi с учетом (5.34), получим выражение
. (5.39)
Последнее соотношение определяет положение уровня Ферми в собственных полупроводниках. При абсолютном нуле (Т =0)
ЕФi = - Еg / 2, (5.40)
т.е. уровень Ферми располагается посередине запрещенной зоны (рис. 5.3, б). С повышением температуры он смещается либо вверх (mp* > mn*), либо вниз (mp* < mn*), либо сохраняет свою высоту (mp* = mn*) (рис. 5.3, б).
Подставляя ЕФi из (5.39) в (5.36) и (5.37), получим выражение, описывающее концентрацию носителей заряда в собственных полупроводниках
. (5.41)
Анализ данного выражения показывает, что равновесная концентрация носителей в полупроводнике определяется шириной запрещенной зоны и температурой полупроводника. Зависимость эта очень сильная. Так, уменьшение Ед с 1,2 эВ (кремний) до 0,08 эВ (серое олово) при комнатной температуре приводит к увеличению концентрации на 9 порядков, а возрастание температуры германия от 100 К до 600 К повышает концентрацию носителей на 17 порядков.
Однако полупроводники часто используют в примесном варианте, т.е. с включением донорной или акцепторной примеси (п. 4.6). Напомним, что в этом случае полупроводники имеют более высокую концентрацию носителей заряда, особенно при низких температурах.
При низких температурах средняя энергия тепловых колебаний кристаллической решетки мала и недостаточна для переброса электрона через запрещенную зону. Однако эта энергия может оказаться достаточной для переходов: донорный уровень – зона проводимости; или валентная зона – акцепторный уровень, т.к. Δ Ед << Еg или Δ Еа << Еg. Поэтому при низких температурах в примесных проводниках происходит возбуждение практически лишь примесных уровней.
Можно считать, что концентрация ионизированных донорных атомов согласно распределению Максвелла-Больцмана равна
, (5.42)
где Nд – концентрация атомов донорной примеси,
а концентрация ионов акцепторной примеси равна
. (5.43)
Для случая низких температур, согласно закону сохранения заряда, соответственно для электронного и дырочного полупроводников можно записать
n = pд, p = nд. (5.44)
Приравнивая (5.37) и (5.42), получим выражения для уровня Ферми в электронном полупроводнике
. (5.45)
Из выражения (5.45) следует, что при нулевой температуре уровень Ферми находится посередине интервала Ед + Ес = Δ Ед и с ростом температуры смещается вниз (рис. 5.4, а).
Если представить последнее выражение в (5.37), то получим формулу для концентрации основных носителей (электронов) в n -полупроводнике
. (5.46)
Представляет интерес и нахождение концентрации неосновных носителей в электронном полупроводнике – дырок pn. Для этого необходимо выражение для уровня Ферми (5.45) подставить в (5.38). После ряда простых преобразований получим закон действующих масс
pnnn = ni2. (5.47)
Из этого закона следует, что при повышении концентрации донорной примеси, а следовательно, и с ростом концентрации основных носителей, наблюдается снижение концентрации неосновных носителей. Закон действующих масс справедлив для любого невырожденного полупроводника в условиях термодинамического равновесия. Так, для дырочного полупроводника можно записать выражение
ppnp = ni2. (5.48)
С повышением температуры полупроводника концентрация носителей (рис. 5.4) возрастает до тех пор, пока она на приблизится к концентрации примеси. Условие электронейтральности в этом случае примет вид nn = Nд. Подставляя в это равенство формулу (5.36), после несложных преобразований получим выражение для уровня Ферми в данном температурном диапазоне
. (5.49)
Дальнейшее повышение температуры приведет к росту концентрации носителей за счет возбуждения их из валентной зоны, а также к росту неосновных носителей. Если концентрация дырок будет близка к концентрации электронов, полупроводник по своим свойствам окажется близким к беспримесному, т.е. p ≈ n, Eфn ≈ Eфi.
Аналогичные рассуждения и выкладки можно провести для полупроводника p-типа, имеющего только акцепторную примесь. В этом случае можно записать выражение для уровня Ферми
(5.50)
и выражение для концентрации основных носителей
. (5.51)
Выражения (5.45), (5.46), (5.50) и (5.51) можно проиллюстрировать соответствующими графиками (рис. 5.4).
|
|
|
а) б)
Рис. 5.4. Зависимость концентрации носителей заряда и уровня Ферми от температуры:
а – электронный полупроводник; б – дырочный полупроводник
На рисунке видно, что при малых температурах уровень Ферми находится между примесным уровнем и краем ближайшей зоны. Концентрация основных носителей при этом резко возрастает с повышением температуры. Затем наступает область, где концентрация основных носителей практически постоянна, а уровень Ферми все время смещается к середине запрещенной зоны. Эту область называют областью истощения примеси, поскольку все имеющиеся атомы ионизированы. В конце данной области начинаются переходы электронов из валентной зоны в зону проводимости и резко возрастает концентрация неосновных носителей.
Если в полупроводнике содержатся оба сорта примесей (доноры и акцепторы), то тип проводимости определяется по преобладающей. Если, например, концентрация доноров больше, чем концентрация акцепторов, то при Т =0 все акцепторные уровни будут заполнены электронами, перешедшими от доноров. Условие электронейтральности в этом случае примет вид
n = pд – Na, (5.52)
где pд по-прежнему определяется из (5.42), а n – из (5.36).
При повышении температуры все донорные уровни опустошаются и концентрация электронов становится постоянной и равной
n = Na – Nд. (5.53)
Все предыдущие рассуждения относятся к слаболегированным полупроводникам, где применима статистика Максвелла-Больцмана. Однако в ряде случаев используются полупроводники с большой концентрацией примеси, т.е. сильнолегированные полупроводники.
На рис. 5.5, а показана температурная зависимость концентрации электронов при различных концентрациях донорной примеси Nд. Рост Nд вызывает естественное смещение графиков вверх, рост температур истощения примеси, а также уменьшение угла наклона примесных участков графиков, т.е. уменьшение энергии ионизации примеси Δ Ед.
Это же происходит и в акцепторных полупроводниках. Например, в кремнии, легированном бором, изменение Δ Еа с ростом Nа описывается эмпирическим соотношением
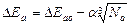, (5.54)
где Еао ≈ 0,08 эВ – энергия ионизации в слаболегированных полупроводниках;
α = 4,3∙10-10 эВ/м.
В соответствии с (5.54) при Nа = 6∙1024 м-3, Δ Еа = 0 и концентрация носителей в примесной области перестает зависеть от температуры. Такие полупроводники называют вырожденными.
|
|
|
а) б) в) г)
Рис. 5.5. Легированные полупроводники: а – температурная зависимость концентрации
носителей; б – примесный уровень в запрещенной зоне; в – примесная зона в запрещенной зоне; г – перекрытие примесной зоны и зоны приводимости в вырожденных полупроводниках
Уменьшение энергии ионизации примеси при увеличении ее концентрации Nпр объясняется тем, что с ростом Nпр расстояние между атомами примеси уменьшается, а взаимодействие между ними растет. При достижении некоторой величины Nпр примесный уровень расщепляется в примесную зону (рис. 5.5, в), а при дальнейшем увеличении Nпр примесная зона растет и может перекрываться с зоной проводимости (рис. 5.5, г). В этом случае энергия ионизации обращается в нуль и полупроводник в примесной области ведет себя, практически как металл. Уровень Ферми с повышением степени легирования смещается к примесной зоне и (в случае вырожденного полупроводника) оказывается, в зависимости от типа примеси, в зоне проводимости или валентной зоне. В области же собственной проводимости полупроводника концентрация его носителей вновь приобретает характерные свойства.
