И проводников. Дырки
Каждая энергетическая зона, как мы уже говорили, содержит ограниченное число энергетических уровней, на каждом из которых может находиться не более двух электронов. Поскольку число электронов в твердом теле тоже ограничено, то согласно принципу минимума свободной энергии заполненными окажутся лишь несколько наиболее низких энергетических зон.
Оказывается, что по характеру зонной модели твердого тела можно определить его электрофизические характеристики. Так, все твердые тела можно поделить на две группы.
К первой группе относятся тела, у которых над целиком заполненными зонами находится зона, заполненная частично (рис. 4.5, а). Такая зона образуется, если верхний уровень атома, из которого зона формируется, тоже заполнен лишь частично. Характерным примером этому могут служить атомы щелочных металлов. Верхняя зона таких элементов, как Li, Na, K заполнена наполовину. Al, Ga, In также имеют частично заполненную валентную зону, хотя являются трехвалентными.
Двухвалентные элементы имеют полностью заполненную валентную зону, однако она перекрывается зоной проводимости (рис. 4.5, б). К ним относятся Be, Mg и др.
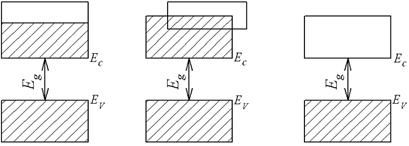
а) б) в)
Рис. 4.5. Зонная структура твердых тел: а, б – проводники,
в – полупроводники и изоляторы
Нужно отметить, что такое заполнение зон у тел первой группы сохраняется и при низких температурах, близких к абсолютному нулю.
Выясним, чем же отличаются твердые тела первой группы. Создадим в кристалле внешнее электрическое поле напряженности ЕЭ. Известно, что такое поле действует на каждый электрон с силой F = eЕЭ, которая стремится нарушить симметрию в распределении электронов по скоростям, пытаясь затормозить электроны, движущиеся против силы, и ускорить электроны, движущиеся вдоль силы. Изменение скорости неизбежно связано с изменением энергии электрона. Такое изменение возможно, если существуют вакантные состояния, т.е. свободные энергетические уровни. Зона должна быть укомплектована не полностью, тогда электрон может принять участие в коллективном перемещении по кристаллу, которое называют электрическим током. Иными словами, твердые тела первой группы являются проводниками, что подтверждают приведенные нами примеры элементов первой группы. Верхнюю зону таких тел называют зоной проводимости.
Важным является то, что электропроводность таких тел сохраняется при очень низких температурах. Кроме того, она имеет температурную зависимость, которая определяется не межзонными переходами, а характером рассеяния электронов и является достаточно невысокой.
Ко второй группе относятся твердые тела, у которых при низких температурах над целиком заполненными зонами находятся пустые зоны (рис. 4.5, в). Типичными примерами таких тел являются элементы четвертой группы таблицы Менделеева Si, Ge, а также ряд химических соединений GaAs, InP, Al2O3 и т.д.
Внешнее поле, приложенное к такому кристаллу, не в состоянии изменить характер движения электронов, т.к. в нижней (валентной) зоне при низких температурах нет свободных состояний, а в верхней зоне – зоне проводимости нет электронов. При повышении температуры твердого тела здесь возможны два варианта, определяемые шириной запрещенной зоны Eg.
Повышение температуры приводит к увеличению тепловой энергии электронов ET ~ kT. Если тепловая энергия становится больше, чем ширина запрещенной зоны
ET > Eg, (4.20)
электрон переходит из валентной зоны в зону проводимости (рис. 4.6, а). В зоне проводимости электрон может изменять свою энергию под действием внешнего поля и участвовать в электропереносе. Одновременно в валентной зоне образуется вакантное состояние, которое может быть занято другим электроном из этой зоны, который также изменяет свою энергию под действием внешнего электрического поля. В обоих случаях перенос заряда осуществляется электронами. Однако проводимость валентной зоны удобно рассматривать как перенос положительного заряда, так называемой “дырки”. Заряд дырки численно равен заряду электрона, а эффективную массу дырки 
мы должны принять численно равной отрицательной эффективной массе электрона 
, который до перехода в зону проводимости занимал это состояние. Только в этом случае ток, создаваемый дырками, будет совпадать как по направлению, так и по величине с током, создаваемым электронами валентной зоны.
а) б)
Рис. 4.6. Процессы генерации (1) и рекомбинации (2) электронно-дырочных пар (а);
б – состояние равновесия: EV – потолок валентной зоны; EC – дно зоны проводимости
Такие твердые тела называют собственными полупроводниками. Как видим, с ростом температуры увеличивается и концентрация носителей заряда, а следовательно, и электропроводность полупроводников. В процессе электропроводности участвуют и электроны, и дырки. Рост концентрации носителей начинается при достижении некоторой пороговой температуры, а электропроводность полупроводников имеет гораздо более сильную температурную зависимость, чем эта зависимость для металлов.
Образование электронно-дырочной пары называют генерацией. Естественно, что при понижении температуры начинает преобладать обратный процесс – рекомбинация, когда дырка и электрон, встречаясь, исчезают. Энергия, затраченная на генерацию пары, при рекомбинации выделяется и передается кристаллической решетке. В случае постоянства температуры наступает динамическое равновесие, когда скорости генерации и рекомбинации равны (рис. 4.6, б).
Очевидно, что в случае невыполнения условия (4.20) генерации носителей не произойдет и твердое тело останется изолятором. Граница между полупроводниками и изоляторами весьма условна и определяется рабочей температурой и шириной запрещенной зоны. Так, у германия, имеющего Eg =0,66 эВ, уже при комнатной температуре концентрация электронов в зоне проводимости достигает величины ni =1019 м-3 и удельное сопротивление составляет всего лишь ρ ≈ 0,5 Ом∙м. В то же время у алмаза, имеющего Eg =5,2 эВ, ni при комнатной температуре оказывается равной только 104 м-3 и ρ ≈ 108 Ом∙м. При такой температуре алмаз является изолятором, но уже при Т =600К концентрация электронов увеличивается на много порядков и проводимость становится сравнимой с проводимостью германия для комнатной температуры. Оксид алюминия Al2O3 имеет Eg =7 эВ и является изолятором во всем диапазоне температур, где он остается твердым телом.
В заключение можно резюмировать вышесказанное:
1. Полупроводники для низких температур являются изоляторами, проводимость в них возникает при повышении температуры или ином сообщении энергии. Излучения, сильные электрические поля и др. способны увеличить концентрацию носителей и электропроводность полупроводников.
2. Разделение тел на полупроводники и изоляторы весьма условно и зависит от рабочей температуры и ширины запрещенной зоны. Для полупроводника Eg <2...3 эВ, для изолятора Eg >6 эВ. Материалы с Eg =3...6 эВ относят к высокотемпературным или широкозонным полупроводникам.
Примесные уровни
В предыдущем разделе речь шла о чистых бездефектных полупроводниках, однако реальные полупроводники любой степени чистоты всегда содержат примесные атомы и другие дефекты. Такие дефекты создают свои собственные энергетические уровни, которые могут располагаться как в разрешенной, так и в запрещенной зонах полупроводника на различной высоте. Особую роль играют уровни, находящиеся в запрещенной зоне, поскольку они существенно влияют на электрические свойства полупроводников. Структурные дефекты всегда являются нежелательными, а примеси в ряде случаев вводят специально для придания полупроводнику требуемых свойств.
Рассмотрим основные типы примесных уровней.
Донорные уровни (от лат. донор – дающий). В качестве донорной примеси в кристалле германия может служить мышьяк. Мышьяк (As) является пятивалентным элементом, а валентность германия равна четырем. Атом мышьяка сходен с атомом германия, только имеет на один электрон больше, поэтому если концентрация примеси невелика, то структура энергетических уровней германия сохранится практически неизменной. Четыре из пяти атомов мышьяка образуют прочную ковалентную связь с четырьмя атомами германия. Пятый электрон не участвует в этой связи. Он находится под действием периодического поля решетки германия и кулоновского поля однозарядного положительного иона мышьяка As+. Притяжение со стороны иона ослабляется полем кристалла – ион можно рассматривать как погруженный в среду с диэлектрической проницаемостью ε. Тогда потенциальное поле иона можно представить в виде
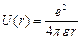. (4.21)
Если подставить функцию (4.21) в уравнение Шредингера, то можно получить формулу для определения энергетического уровня пятого электрона
, (4.22)
где me – масса покоя электрона.
В формуле (4.22) энергия Δ Eд измеряется в эВ и отсчитывается от дна зоны проводимости. Видно, что энергетический уровень пятого электрона лежит ниже зоны проводимости, т.е. находится в запрещенной зоне (рис. 4.6, а). Для германия обычно m */ me =0,12 и расчет Δ Eд =-0,006 эВ. Более точная теория дает Δ Eд =-0,008 эВ, а результат эксперимента показывает Δ Eд =-0,013 эВ, что является хорошим соответствием.
При сообщении пятому электрону даже небольшой энергии он отрывается от атома и переходит в зону проводимости, оставляя на примесном уровне положительный ион, вследствие чего такую примесь называют донорной, а примесный уровень – Ед (рис. 4.7, а). Температура, при которой происходит ионизация примеси, гораздо ниже температуры генерации электронно-дырочных пар в собственном полупроводнике, поскольку Δ Ед << Eg. В этом случае концентрация основных носителей заряда – электронов гораздо выше концентрации неосновных носителей – дырок, т.е. nn >> pn.
В полупроводнике с донорной примесью вначале растет концентрация только электронов, а при более высоких температурах начинается и генерация электронно-дырочных пар. Положительные ионы примеси, в отличие от дырок, не принимают участия в электропереносе, поскольку “встроены” в кристаллическую решетку.
а) б) в)
Рис. 4.7. Примесные уровни в полупроводниках: а – донорный уровень; б – акцепторный уровень; в – уровни прилипания (ЕП) и более глубокие уровни (ЕЛ)
Полупроводники, где основными носителями являются электроны, называют электронными, или n-полупроводниками. В табл. 4.1. приведены примеры донорной примеси для элементарных полупроводников германия и кремния.
Таблица 4.1
Донорные примеси
| Полупроводник | Энергия ионизации Δ Ед, эВ | ||
| фосфор | мышьяк | сурьма | |
| германий | 0,012 | 0,013 | 0,010 |
| кремний | 0,045 | 0,050 | 0,039 |
Акцепторные уровни (от лат. акцептор – принимающий). Предположим, что в решетке германия часть атомов замещена атомами трехвалентного индия, которые образуют по три связи с атомами германия и формируют акцепторный уровень – Еа. Четвертая связь остается неполной, для нее у атома индия не хватает одного электрона. Такой электрон может быть захвачен у атома германия. Тогда атом индия превращается в отрицательный ион, а на месте захваченного электрона возникает дырка (рис. 4.7, б). Поскольку ионы индия не могут перемещаться по кристаллу, в электропереносе участвуют только дырки. Такой полупроводник называют дырочным, или p-полупроводником. Основными носителями в p-полупроводнике являются дырки, а неосновными – электроны. Расчет показывает, что для ионизации атома индия требуется энергия Δ Еа ≈ 0,01 эВ, т.е. температура перехода уровень-зона гораздо меньше, чем температура межзонного перехода.
В табл. 4.2 приведены энергии ионизации акцепторных атомов.
Донорные и акцепторные примеси могут присутствовать в полупроводнике одновременно. В этом случае запрещенная зона будет содержать два типа примесных уровней, а полупроводник – дырки и электроны одновременно. Возможно создание компенсированного полупроводника, где как в собственном полупроводнике будет выполняться условие n = p.
Таблица 4.2
Акцепторные примеси
| Полупроводник | Энергия ионизации Δ Еа, эВ | |||
| бор | алюминий | галлий | индий | |
| германий | 0,010 | 0,010 | 0,011 | 0,011 |
| кремний | 0,045 | 0,060 | 0,070 | 0,160 |
Из данных таблиц видно, что донорные и акцепторные уровни являются мелкими, т.е. Δ Е << Eg. Уровни прилипания также относятся к мелким уровням. Они находятся еще ближе к зоне проводимости или валентной зоне. По своей сути уровни прилипания являются донорными или акцепторными уровнями, но электрон, захваченный таким уровнем EП, не остается там длительное время, а, вследствие теплового возбуждения, вновь перебрасывается в зону. Аналогичный обмен дырками происходит между валентной зоной и близким к ней уровнем прилипания (рис. 4.7, в).
Наличие в полупроводнике уровней прилипания может существенно увеличить время жизни неравновесных носителей заряда.
Глубокие примесные уровни ЕЛ образуются вблизи середины запрещенной зоны при легировании полупроводника некоторыми элементами (рис. 4.7, в). Примерами таких глубоких уровней являются энергетические уровни, образованные в кремнии атомами третьей группы таллия (акцепторный уровень, Δ Еа =0,26 эВ) или атомами элемента переходной группы марганца (донорный уровень, Δ Ед =-0,53 эВ). Глубокие уровни играют большую роль в процессах рекомбинации неравновесных носителей заряда.
Приведенные выше рассуждения справедливы лишь для малой концентрации примесей, когда взаимодействием примесных атомов между собой можно пренебречь. В этом случае примесный уровень является дискретным (см. рис. 4.7). С увеличением концентрации примесей необходимо учитывать расщепление примесных уровней в соответствии с постулатом Паули и образование примесных зон. При большой степени легирования примесная зона может настолько расширится, что перекроется с ближайшей энергетической зоной полупроводника.
Структурные дефекты в полупроводниках образуют локальные уровни, играющие роль донорных или акцепторных. Примерами таких дефектов являются дефекты по Шоттки, по Френкелю, дислокации. Поверхность полупроводника образует ряд поверхностных энергетических уровней, имеющих большое практическое значение (п. 7.5).
Контрольные вопросы и задания
1.1. Что произойдет при сближении атомов?
1.2. Как и почему изменяются энергетические уровни в кристаллах?
1.3. Какие электроны становятся общими для кристалла?
1.4. Каково расстояние между уровнями в разрешенной зоне?
1.5. Покажите отличия в энергетическом спектре двух, четырех, восьми атомов Zn.
1.6. Поясните смысл функции ρ (r).
2.1. Какова структура модели Кронига-Пенни?
2.2. Поясните смысл одноэлектронного приближения.
2.3. Поясните смысл адиабатического приближения.
2.4. Что представляет собой функция Блоха?
2.5. Охарактеризуйте функцию E (k) для кристалла.
3.1. Какие зоны называют зонами Бриллюэна?
3.2. Охарактеризуйте приведенные зоны Бриллюэна.
3.3. Нарисуйте дисперсионную кривую для кремния.
3.4. Нарисуйте дисперсионную кривую для германия.
3.5. Что называют потолком валентной зоны, дном зоны проводимости?
4.1. Определите понятие эффективной массы электрона.
4.2. Определите понятие эффективной массы дырки.
4.3. Почему функция m *(k) имеет разрывы?
4.4. В чем заключается смысл “отрицательности” эффективной массы дырки?
4.5. Запишите выражение для эффективной массы электрона.
4.6. Приведите условия возрастания эффективной массы электрона.
5.1. Какую зонную структуру имеют проводники? Почему?
5.2. Опишите зонную структуру изолятора.
5.3. Опишите зонную структуру полупроводника.
5.4. В чем различие зонных структур изолятора и полупроводника?
5.5. Приведите примеры изолятора и полупровдника при 20°С.
5.6. Какую зонную структуру должны иметь полупроводники и изоляторы, если Т =700К?
6.1. Как формируются донорные уровни?
6.2. Как формируются акцепторные уровни?
6.3. Оцените величину энергии ионизации примеси при Т =300К.
6.4. Какие элементы относятся к донорным (акцепторным) примесям?
6.5. Что представляют собой глубокие примесные уровни?
6.6. Что представляют собой уровни прилипания?
6.7. Когда образуются примесные зоны?
6.8. Какие еще дефекты образуют энергетические уровни?
Глава 5
ЭЛЕКТРОПРОВОДНОСТЬ ТВЕРДЫХ ТЕЛ
Электрофизические свойства твердых тел, явления в них, а особенно, в контактах различных тел лежат в основе работы микроэлектронных устройств. В традиционной электронике основная доля устройств использует эффекты, связанные с электропроводностью.
Электропроводность характеризует одно из явлений переноса, а именно, перенос носителей заряда.
