| N(x)R(y)dx+M(x)K(y)dy=0 (1)
|
| Это ур-ие наз. Ур-ем с разделяющимися переменными. Метод его решения: разделив (1) на произведение M(x)K(y)
|
| получим
|
| N(x)/M(x)*dx+K(y)/R(y)*dy=0 (2)
|
| Уравнение (2) наз. Ур-ем с разделенными переменными. Операция деления уравнения (1) на произведение М(х)R(y)
|
| Наз. разделением переменных. Интегрируя (2), получим общий интеграл
|
| ∫(N(x)/M(x)*dx)+ ∫(K(y)/R(y)*dy)=0 исходного уравнения. При делении (1) на произведение М(х)R(y), можно потерять некоторые решения, которые получаются из уравнения
|
| М(х)R(y)=0
|
| Определяя из этого уравнения решения y=ϕ(x), следует проверить, является ли оно решением уравнения (1). Если не является, его следует отбросить, а если является, то проверить, входит ли оно в общий интеграл.
|
| Если входит, то оно есть частное решение, а если не входит, то это решение называется особым.
|
| Пример. Решить уравнение y(x+1)dx+(y-1)xdy=0.
|
| Решение. Разделим уравнение на произведение xy, получим:
|
| (x+1)/x*dx+(y+1)/y*dy=0;
|
| dx+(dx/x)+dy+ (dy/y)=0
|
| Интегрируя получим общий интеграл
|
| x+ln|x|+y+ln|y|=c;
|
| ln|xy|+x+y=c.
|
| В этом уравнении М(х)R(y) имеет вид xy=0. Его решения x=0, y=0
|
| является решениями исходного уравнения, но не входит в общий интеграл.
|
| Следовательно, решения x=0, y=0 является особыми.
|
ДУ полных диф-лов
Рассмотрим диф. уравнение вида: 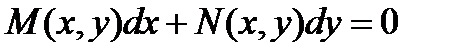 (1). Если левая часть этого уравнения явл. полным дифференциалом некоторые ф-ции 2-х переменных U(x,y), т е M(x,y)dx+N(x,y)=du (2), то это уравнение называется уравнением в полных диф. Тогда ур-ние (1) принимает вид du(x,y)=0. Общим интегралом этого ур-ния будет равенство U(x,y)=C=const. Втесним условие, при кот ур-ние (1) явл. ур-нием в полных диф. Выражение для полного диф. ф-ции 2-х переменных имеем вид (1). Если левая часть этого уравнения явл. полным дифференциалом некоторые ф-ции 2-х переменных U(x,y), т е M(x,y)dx+N(x,y)=du (2), то это уравнение называется уравнением в полных диф. Тогда ур-ние (1) принимает вид du(x,y)=0. Общим интегралом этого ур-ния будет равенство U(x,y)=C=const. Втесним условие, при кот ур-ние (1) явл. ур-нием в полных диф. Выражение для полного диф. ф-ции 2-х переменных имеем вид  (3). Сравнивая (2) и (3), имеем: (3). Сравнивая (2) и (3), имеем:  , ,  . Дифференцируем первое из этих равенств по у, а второе – по х, имеем: . Дифференцируем первое из этих равенств по у, а второе – по х, имеем:  , ,  отсюда, предполагая непрерывность вторых произвольных, получаем отсюда, предполагая непрерывность вторых произвольных, получаем  (4) – условие, когда данное уравнение явл. уравнением полных диф. (4) – условие, когда данное уравнение явл. уравнением полных диф.
|
60.1.ДУ вида dy/dx=f(ax+by+c)
| Имеем ф-цию z=ax+by+c.(2)Продиф-м обе части по х:dz/dx=a+b*dy/dx.Подставляем dy/dx из исх-го ур-ия (1).Имеем dz/dy=a+bf(ax+by+c) или с учетом (2) имеем dz/dx=a+bf(z).Это ур-ие явл. ур-ем с разд-ся переменными.
|
| dx=dz/(a+bf(z))
|
| x=(∫dz//(a+bf(z)))+c-общее решение ДУ
|
Уравнения Бернулли
| 62. Уравнение Бернулли
|
Это ур-ние имеет вид:  (7). Это ур-ние сводится к лин. уравнению (7). Это ур-ние сводится к лин. уравнению  (7а). Сделаем замену переменной: (7а). Сделаем замену переменной:  (8), (8),  . Подставляем это в (7а), получаем: . Подставляем это в (7а), получаем:  - получение лин. уравнения, кот можно решать, например, методом вариации постоянной. - получение лин. уравнения, кот можно решать, например, методом вариации постоянной.
|
61.1.ДУ вида dy/dx=f(y/x)
| Такое ур-ие приводится к ур-ию с разделяющимися переменными при помощи замены
|
| u=y/x(1)
|
| y=u*x(2)
|
| y,=u,x+u(3)
|
| Подст.(3) и (2) в (1), имеем u,x+u=f(u) (4)
|
| du/dx*x=f(u)-u разделяем на dx получаем остаток x(f(u)-u)
|
| du/(f(u)-u)=dx/x
|
| Интегрируем обе части ∫(du/(f(u)-u))=lnIxI+c
|
Линейные ДУ 1-го порядка
Общий вид лин. уравнения 1-ого порядка  (1) (1)   Если правая часть уравнения равна 0 Если правая часть уравнения равна 0  =0, то соответственно уравнение называется линейным однородным уравнением. =0, то соответственно уравнение называется линейным однородным уравнением.   (2). Если же правая часть не равна 0, то уравнение назыв. неоднородным. Решим сначала неоднородное уравнение (2). В этом урав-ии переменные разделяются: (2). Если же правая часть не равна 0, то уравнение назыв. неоднородным. Решим сначала неоднородное уравнение (2). В этом урав-ии переменные разделяются:  = - р(х)у, = - р(х)у,  = - р(х)dx. Интегрируем обе части, имеем: = - р(х)dx. Интегрируем обе части, имеем:  , ,
|
ln  = =  , y = C*e , y = C*e  (3) – это общее решение однородного уравнения (2). (3) – это общее решение однородного уравнения (2).
|
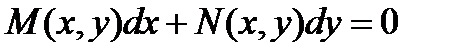 (1). Если левая часть этого уравнения явл. полным дифференциалом некоторые ф-ции 2-х переменных U(x,y), т е M(x,y)dx+N(x,y)=du (2), то это уравнение называется уравнением в полных диф. Тогда ур-ние (1) принимает вид du(x,y)=0. Общим интегралом этого ур-ния будет равенство U(x,y)=C=const. Втесним условие, при кот ур-ние (1) явл. ур-нием в полных диф. Выражение для полного диф. ф-ции 2-х переменных имеем вид
(1). Если левая часть этого уравнения явл. полным дифференциалом некоторые ф-ции 2-х переменных U(x,y), т е M(x,y)dx+N(x,y)=du (2), то это уравнение называется уравнением в полных диф. Тогда ур-ние (1) принимает вид du(x,y)=0. Общим интегралом этого ур-ния будет равенство U(x,y)=C=const. Втесним условие, при кот ур-ние (1) явл. ур-нием в полных диф. Выражение для полного диф. ф-ции 2-х переменных имеем вид  (3). Сравнивая (2) и (3), имеем:
(3). Сравнивая (2) и (3), имеем:  ,
,  . Дифференцируем первое из этих равенств по у, а второе – по х, имеем:
. Дифференцируем первое из этих равенств по у, а второе – по х, имеем:  ,
,  отсюда, предполагая непрерывность вторых произвольных, получаем
отсюда, предполагая непрерывность вторых произвольных, получаем  (4) – условие, когда данное уравнение явл. уравнением полных диф.
(4) – условие, когда данное уравнение явл. уравнением полных диф.
 (7). Это ур-ние сводится к лин. уравнению
(7). Это ур-ние сводится к лин. уравнению  (7а). Сделаем замену переменной:
(7а). Сделаем замену переменной:  (8),
(8),  . Подставляем это в (7а), получаем:
. Подставляем это в (7а), получаем:  - получение лин. уравнения, кот можно решать, например, методом вариации постоянной.
- получение лин. уравнения, кот можно решать, например, методом вариации постоянной.
 (1)
(1) 
 Если правая часть уравнения равна 0
Если правая часть уравнения равна 0  =0, то соответственно уравнение называется линейным однородным уравнением.
=0, то соответственно уравнение называется линейным однородным уравнением. 
 (2). Если же правая часть не равна 0, то уравнение назыв. неоднородным. Решим сначала неоднородное уравнение (2). В этом урав-ии переменные разделяются:
(2). Если же правая часть не равна 0, то уравнение назыв. неоднородным. Решим сначала неоднородное уравнение (2). В этом урав-ии переменные разделяются:  = - р(х)у,
= - р(х)у,  = - р(х)dx. Интегрируем обе части, имеем:
= - р(х)dx. Интегрируем обе части, имеем:  ,
,
 =
=  , y = C*e
, y = C*e  (3) – это общее решение однородного уравнения (2).
(3) – это общее решение однородного уравнения (2).






