Рассмотрим на отрезке 
задачу Коши для нелинейного обыкновенного дифференциального уравнения первого порядка 
(1) с начальным условием 
.(2)
Пусть задача Коши (1), (2) имеет единственное решение 
. На отрезке 
зададим последовательность точек
(3)
Говорят, что на отрезке введена сетка. Сетка – это конечное множество точек, в данном случае, на отрезке. Точки 
называют узлами сетки. Узлы 
называют граничными, остальные узлы сетки – внутренними. Если расстояние 
между соседними узлами сетки не одинаково, то говорят, что задана неравномерная сетка. Если же 
, то говорят, что на отрезке задана равномерная сетка с шагом 
. В численных методах решения задачи Коши приближенное решение ищется в виде таблицы чисел 
, приближающих значения 
точного решения в узлах сетки. Расчетные формулы численных методов решения задачи Коши в большинстве случаев можно представить в виде 
. (4) Здесь функция 
опр-ся выбором сетки и способом построения метода. Если 
, 
, то расчетная формула (4) принимает вид 
. (5). Такие методы называют явными одношаговыми. Если , 
, то расчетная формула (4) принимает вид 
. (6). Соотв-ий метод называют неявным одношаговым. В случае когда в расчетной формуле (4) 
или 
, методы называют многошаговыми. При 
многошаговые методы, как и одношаговые, называются явными, а при 
- неявными.
Методы Эйлера, трапеций и Коши-Эйлера.
Рассмотрим задачу Коши для нелинейного о. д. у. первого порядка: 
, (7) . (8)
На отрезке введем сетку 
(9)
Геометр. вывод расчетной формулы метода Эйлера.
Пусть найдено уже приближение 
к решению 
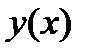задачи (7), (8) в узле 
сетки (9). Обозначим через 
интегральную кривую дифференциального уравнения (7), проходящую через точку 
. Проведем к этой интегральной кривой касательную в точке 
до пересечения с вертикалью 
в точке 
и ординату точки возьмем в качестве приближения 
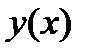к решению задачи (7), (8) в узле 
.
Из прямоугольного треугольника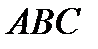 
найдем выражение для вычисления
.
Получили для решения задачи Коши (7), (8) расчетную формулу метода Эйлера: 
(10)
Аналитич. вывод расчетной формулы метода Эйлера.
Проведем разложение в ряд Тейлора (11)
Из этого разложения с учетом, что 
и 
, получаем снова расчетное правило метода Эйлера 
. (10)
Метод Эйлера является одношаговым и явным. Из формул (10) и (11) для погрешности 
метода Эйлера на шаге следует оценка
, (11)
где 
- максимальное значение вторых производных для интегральных кривых, лежащих в рассматриваемой окрестности решения 
.
Погрешность одношагового метода 
есть величина на единицу меньшего порядка относительно 
по сравнению с погрешностью на шаге (11). Таким образом, метод Эйлера относится к численным методам первого порядка точности.
Использование квадратурных формул для построения численных методов решения задачи Коши.
Расчетную формулу (10) метода Эйлера можно получить также, применяя квадратурную формулу левых прямоугольников к интегралу в формуле Ньютона-Лейбница 
. (12)
Если применить к вычислению интеграла в (10) квадратурную формулу трапеций, то получим расчетное правило 
(13) неявного метода Адамса второго порядка точности или метода трапеций.
Расчетная формула (11) представляет собой уравнение с одним неизвестным 
. Если начальное приближение вычислить по методу Эйлера и сделать одну итерацию при решении уравнения (13), то получим расчетную формулу 
(8)
метода Коши-Эйлера. Это явный метод второго порядка точности.
