Идею метода Ритца рассмотрим на примере простейшей вариационной задачи
 , (1)
, (1)
 . (2)
. (2)
Будем считать, что вариационная задача (1), (2) имеет решение  :
:  .
.
Последовательность функций  называют минимизирующей, если
называют минимизирующей, если  . Основная идея метода Ритца заключается в сведении вариационной задачи к задаче на отыскание минимума функции. Пусть имеется семейство функций
. Основная идея метода Ритца заключается в сведении вариационной задачи к задаче на отыскание минимума функции. Пусть имеется семейство функций  , таких, что при любых конечных значениях числовых параметров
, таких, что при любых конечных значениях числовых параметров  каждая функция
каждая функция  принадлежит
принадлежит  . Тогда
. Тогда
 и возникает задача нахождения значений
и возникает задача нахождения значений  параметров, при которых функция
параметров, при которых функция  принимает минимальное значение. Если функция непрерывно дифференцируема по своим аргументам, то можно воспользоваться принципом Ферма и определить искомые значения параметров
принимает минимальное значение. Если функция непрерывно дифференцируема по своим аргументам, то можно воспользоваться принципом Ферма и определить искомые значения параметров  из системы уравнений
из системы уравнений  . (3). В методе Ритца в качестве
. (3). В методе Ритца в качестве  -го приближения к решению
-го приближения к решению 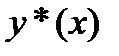 вариационной задачи (1), (2) берется функция
вариационной задачи (1), (2) берется функция  .
.
Семейство функций  , называется
, называется  -полным на
-полным на  , если для
, если для  ,
,  , такие, что
, такие, что  .
.
Теорема. Если функция  непрерывна в области
непрерывна в области  и семейство функций
и семейство функций  является
является  -полным на
-полным на  , то последовательность
, то последовательность  , построенная по Ритцу минимизирующая.
, построенная по Ритцу минимизирующая.
Доказательство. Зададимся произвольным положительным числом  . В силу непрерывности
. В силу непрерывности 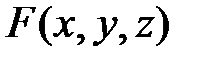 , существует
, существует  , такое,что
, такое,что
 при
при  .
.
Поскольку система функций  является
является  -полной на
-полной на  , то для
, то для 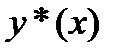
 , такие, что функция
, такие, что функция  удовлетворяет неравенствам
удовлетворяет неравенствам
 при
при  . Таким образом,
. Таким образом,
 .
.
Учитывая, что  , отсюда имеем
, отсюда имеем  . Так как
. Так как  произвольно, то окончательно получаем
произвольно, то окончательно получаем  . Теорема доказана.
. Теорема доказана.
Для функционала  (4) имеет место
(4) имеет место
Теорема. Если последовательность  является минимизирующей для вариационной задачи (4), (2), то она сходится к решению этой задачи.
является минимизирующей для вариационной задачи (4), (2), то она сходится к решению этой задачи.
Доказательство. Элемент  минимизирующей последовательности приближает решение
минимизирующей последовательности приближает решение 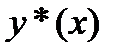 вариационной задачи с погрешностью
вариационной задачи с погрешностью
 .
.
Применяя к последнему интегралу неравенство Буняковского, имеем
 .
.
Учитывая, что 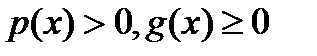 на
на  , получаем
, получаем

Учитывая  , получаем окончательную оценку
, получаем окончательную оценку
 , из которой следует утверждение теоремы.
, из которой следует утверждение теоремы.
Вариационно-разностный вариант метода Рица.
Решение вариационной задачи
 (1)
(1)
 . (2)
. (2)
методом Ритца заключается в построении минимизир. последовательности  . (3) Значения параметров
. (3) Значения параметров  находятся из системы линейных алгебраических уравнений
находятся из системы линейных алгебраических уравнений  , (4) коэффициенты которой вычисляются по формулам
, (4) коэффициенты которой вычисляются по формулам
 (5)
(5)
 . (6)
. (6)
Следовательно, основной объем вычислений при решении вариационной задачи (1), (2) методом Рица приходится на вычисления по формулам (5), (6) и решение системы (4). Уменьшить объем вычислений можно за счет рац. выбора корд. ф-ий. На отрезке  построим сетку
построим сетку
 . (7) и зададим последовательность координатных функций
. (7) и зададим последовательность координатных функций
 и
и 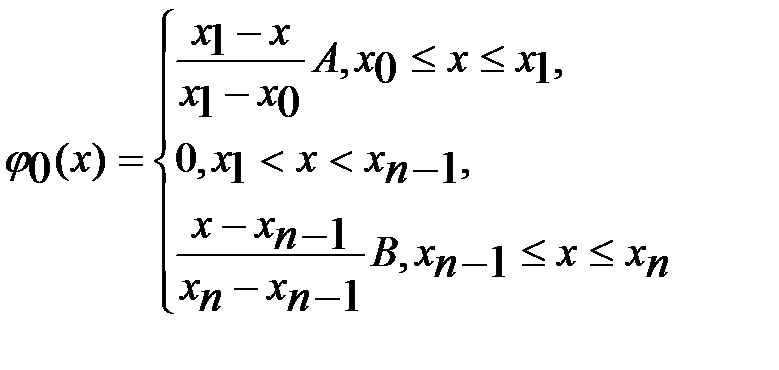 (8). При таком задании координатных функций для значений минимизир. посл-ти ф-ий (3) во внутр. узлах сетки получаем
(8). При таком задании координатных функций для значений минимизир. посл-ти ф-ий (3) во внутр. узлах сетки получаем
 След-но, значения парам. имеют смысл приближений
След-но, значения парам. имеют смысл приближений  к решению во внутренних узлах сетки и формулы (3) и (4) можно переписать в виде
к решению во внутренних узлах сетки и формулы (3) и (4) можно переписать в виде
 (3’),
(3’),  (4’).
(4’).
Подставим в расчетные формулы (5) и (6) заданные координатные функции (8). Получаем  при
при  ,
,

 ,
,

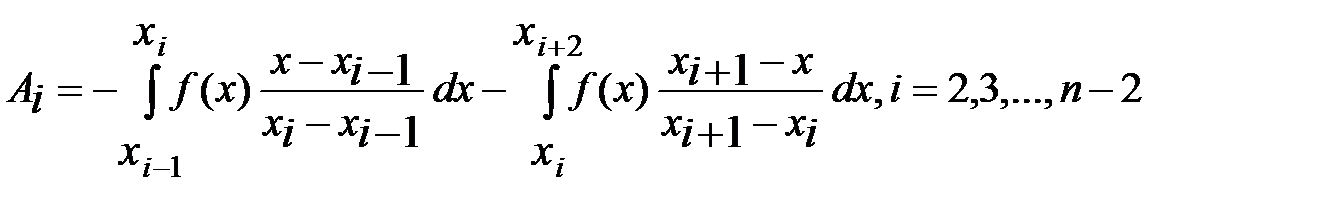
 Система (4¢) в данном случае является симметричной и трехдиагональной
Система (4¢) в данном случае является симметричной и трехдиагональной 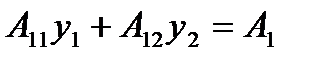 ,
,  ,
,  .
.
58. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
Краевая задача  , (1)
, (1)
 (2) эквивалентна вариационной задаче
(2) эквивалентна вариационной задаче
 (3)
(3)
 . (4)
. (4)
Сначала зададим семейство функций  , которое было бы
, которое было бы  -полным на
-полным на  , а затем построим минимизирующую последовательность
, а затем построим минимизирующую последовательность  , где значения параметров опр-ся из системы вида
, где значения параметров опр-ся из системы вида  . (5). Выберем последовательность функций
. (5). Выберем последовательность функций  так, чтобы выполнялись следующие условия:
так, чтобы выполнялись следующие условия:
1) 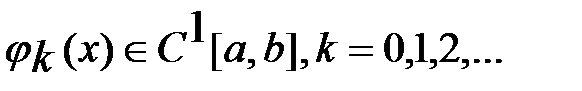 ;
;
2)  ;
;
3) функции  линейно независимы;
линейно независимы;
4) система функций  , образованных по правилу
, образованных по правилу 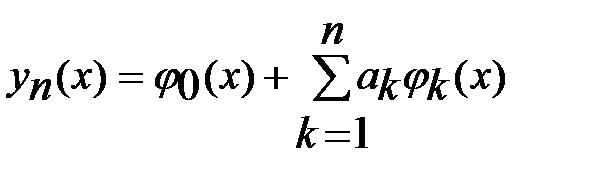 является
является  - полной на
- полной на  .
.
Очевидно, коэффициенты  при
при  можно трактовать, как координаты функции
можно трактовать, как координаты функции  . Поэтому функции
. Поэтому функции  называют координатными. Имеем
называют координатными. Имеем
 Система (5) в данном случае получается в виде (6)
Система (5) в данном случае получается в виде (6)
 Систему можно записать в стандартной форме
Систему можно записать в стандартной форме
 , где коэффициенты определяются формулами
, где коэффициенты определяются формулами 
Теорема. Если 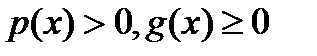 на
на  , то система (6) имеет единственное решение.
, то система (6) имеет единственное решение.
Доказательство. Рассмотрим однородную систему, соответствующую (6): 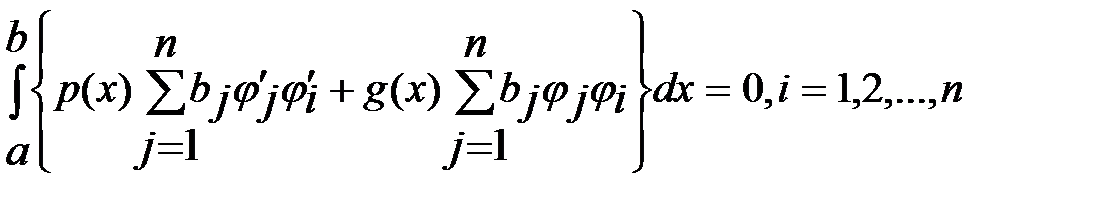
Умножим каждое уравнение системы на соответствующее  и просуммируем получившиеся уравнения. В результате получим
и просуммируем получившиеся уравнения. В результате получим

В силу положительности  отсюда следует
отсюда следует  и
и  . Таким образом,
. Таким образом,  , поскольку координатные функции линейно независимы. Следовательно, рассматриваемая однородная система имеет только тривиальное решение, ее определитель отличен от нуля и соответствующая неоднородная система имеет единственное решение при любых правых частях уравнений. Теорема доказана.
, поскольку координатные функции линейно независимы. Следовательно, рассматриваемая однородная система имеет только тривиальное решение, ее определитель отличен от нуля и соответствующая неоднородная система имеет единственное решение при любых правых частях уравнений. Теорема доказана.
В качестве координатных функций на практике часто берут функции: 1)  или
или  ; 2)
; 2) 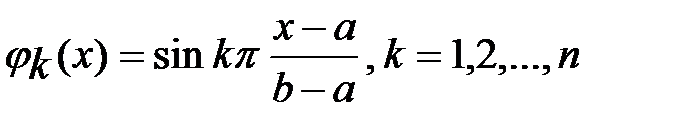 . При этом в обоих случаях для обеспечения выполнения граничных условий берут функцию
. При этом в обоих случаях для обеспечения выполнения граничных условий берут функцию  . Легко видеть, что система функций
. Легко видеть, что система функций  принадлежит множеству
принадлежит множеству  допустимых функций. Доказательство
допустимых функций. Доказательство  -полноты на
-полноты на  системы функций с координатными функциями первого вида проведем сначала для случая нулевых граничных условий
системы функций с координатными функциями первого вида проведем сначала для случая нулевых граничных условий  . Возьмем
. Возьмем 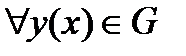 и
и  . Для
. Для  существует многочлен
существует многочлен  степени
степени  , такой, что
, такой, что  . Рассмотрим многочлен степени
. Рассмотрим многочлен степени  :
:  . Он принадлежит множеству
. Он принадлежит множеству  . Для производных на отрезке справедлива оценка
. Для производных на отрезке справедлива оценка 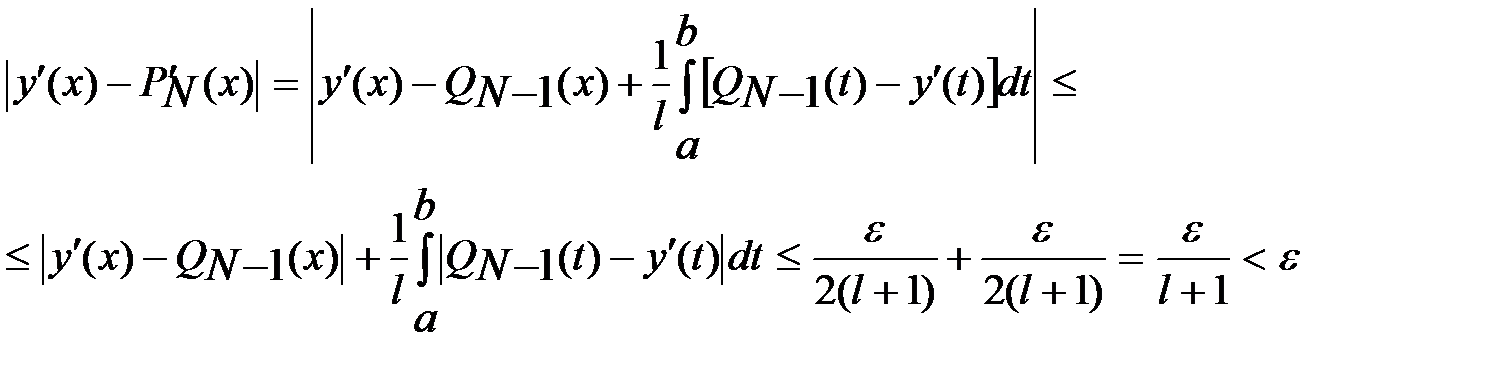
Проведем оценку приближения на отрезке функции  многочленом
многочленом 

Обозначим  . Отсюда
. Отсюда  . Таким образом, многочлен
. Таким образом, многочлен  представляется в виде
представляется в виде  . Рассмотрим теперь случай ненулевых граничных условий. Возьмем
. Рассмотрим теперь случай ненулевых граничных условий. Возьмем 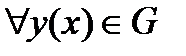 и
и  . Для функции
. Для функции  построим указанным выше способом многочлен
построим указанным выше способом многочлен  , для которого выполняются неравенства
, для которого выполняются неравенства 
Таким образом, многочлен  и его производная приближают соответственно функцию
и его производная приближают соответственно функцию  и ее производную с погрешностью, не превышающей
и ее производную с погрешностью, не превышающей  .
.






