4.1 Построение эпюр внутренних усилий в раме.
Рамой называется ломаный стержень, состоящий стоек и ригелей, соединенных жесткими или шарнирными узлами (рис. 4.1).

В плоских рамах, в отличии от балок, возникают три внутренних усилия: М – изгибающий момент, Q – поперечная сила и N – продольная сила, которые определяются методом сечений. Напомним, что изгибающий момент в сечении равен сумме моментов всех сил, приложенных к оставшейся части, относительно центра тяжести рассматриваемого сечения. Поперечная сила равна сумме проекций тех же сил на поперечную ось стержня, а продольная сила равна сумме проекций этих же сил на продольную ось стержня.
Порядок построения эпюр:
1. Определяются опорные реакции (для консольных стержней (рис. 4.1,б) можно обойтись без определения реакций).
2. Рама разбивается на участки. Границами участков служат точки приложения сосредоточенных сил или моментов, начало и конец распределенной нагрузки, узлы рамы.
3. Для каждого участка записываются выражения для внутренних усилий, производится вычисление этих усилий в пределах участка.
4. Выбирается масштаб эпюр таким образом, чтобы наибольшая ордината не превышала 1/3 ÷ 1/4 габарита рамы, и строятся эпюры M, Q, N. Эпюры Q, N строятся в одном масштабе.
5. Делается проверка построенных эпюр на соответствие приложенной нагрузки и по равновесию узлов рамы, рамы в целом.
|
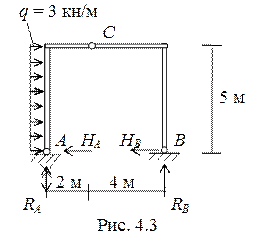
Пример 4.1 Построить эпюры внутренних усилий в трехшарнирной раме (рис. 4.2).

|
1. Обозначим в соответствии с видом опор опорные реакции (рис. 4.3) и определяем их значение, используя уравнения равновесия.
Σ mA = 0, - q ··5∙2.5 + RB ·6 = 0. RB = 6.25 кН.
Σ mВ = 0, - q ·5·2.5 - RА ·6 = 0. RА = - 6.25 кН. Меняем направление реакции RА и считаем ее положительной (RА = 6,25кН) и направленной в низ.
Учитывая, что в шарнире С изгибающий момент отсутствует, можно записать:
Σ mCпр = 0. RB ·4 - HB ·5 = 0, HB = 5 кН.
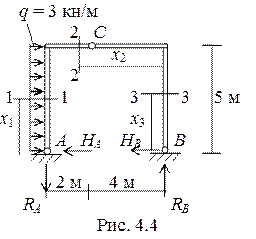
|
Σ mCлев = 0. RА ·2 + q· 5 · 2.5 – HA ·5 = 0, HA = 10 кН.
Проверка.
Σ х = 0. q ·5 - HA - HB = 0.
Σ y = 0. - RA + RB = 0.
2. Обозначаем участки (рис. 4.4). В качестве «оставшейся части» оставляем ту часть рамы, к которой приложено меньше усилий.
Правила знаков, применяемые при построении эпюр внутренних усилий:

3. Записываем выражения для внутренних усилий.
1-й участок, 0 < х 1 < 5 м.
N 1 = RA = 6.25 кН.
Q 1 = HA - q∙x 1, Qx= 0 = HA = 10 кН, Qx= 5 = HA = 10 - 3∙5 = - 5 кН.
М 1 = - HA∙x 1 + q∙x 1 ∙x 1/2. Получили уравнение квадратной параболы. Для ее построения необходимо вычислить три значения момента.
Мх = 0 = 0, Мх = 5 = - 10∙5 + 3∙52/2 = - 12,5 кНм,
Мх = 2,5 = - 10∙2,5 + 3∙(2,5)2/2 = - 15,6 кНм.
2-й участок, 0 < х 2 < 6 м.
N 1 = - HB = - 5 кН.
Q 1 = - RB = - 6.25 кН.
М 1 = - HB∙ 5 + RB∙x 2. Мх = 0 = - 25 кНм, Мх = 6 = - 25 + 6,25∙6 = 12,5 кНм,
2-й участок, 0 < х 3 < 5 м.
N 1 = - RB = - 6.25 кН.
Q 1 = HB = 5 кН.
М 1 = - HB∙x 3. Мх = 0 = 0, Мх = 5 = - 25 кНм,
4. Строим эпюры (рис. 4.6)

|
5. Проверяем равновесие узлов. Вырежем поочередно узлы рамы с действующими в их элементах внутренними усилиями, и запишем для них уравнения равновесия (рис. 4.7). При проверке моментов пунктиром отмечены растянутые волокна.

На рисунке 4.7 видно, что все уравнения равновесия (Σ х = 0, Σ y = 0, Σ m = 0) для узлов выполняются.
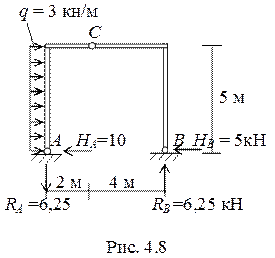
Осуществим проверку равновесия рамы в целом (рис. 4.8). Для этого восстановим значения реакций, используя эпюры внутренних усилий.
|
В точке А вертикальная реакция будет направлена вниз, поскольку левая стойка растянута, а правая реакция (т. В) направлена вверх, т. к. правая стойка сжата.
Обе горизонтальные реакции в опорах · А и В будут направлены влево, поскольку по знаку эпюры Q (знак «+») они должны вращать элемент по часовой стрелке.
Записываем уравнения равновесия:
Σ х = 0. q ·5 - HA - HB = 3∙5 – 10 – 5 = 0.
Σ y = 0. - RA + RB = - 6,25 + 6,25 = 0.
Σ m A = 0, - q ·5·2.5 + RB 6 = 3·5·2.5 – 6.25·6 =
= - 37.5 + 37.5 = 0.






