Расчет ферм на подвижную нагрузку сводится к построению линий влияния при действии на ферму подвижной единичной силы, перемещающейся по одному из поясов.
Порядок построения линий влияния в фермах рассмотрим на примере. Рассмотрим построение линий влияния усилий N 35, N 34, N 45, и N 67 для фермы, показанной на рис. 2. 9.
Для построения линии влияния (а это график) усилия в стержне 3-5 необходимо получить выражение для этого усилия в зависимости от положения единичной силы. В свою очередь, единичная сила Р = 1 перемещается по нижнему поясу – это отмечено на ферме пунктирной линией. Для определения усилия N 35 разрежем вторую панель сечением I-I и воспользуемся методом моментной точки. Моментной точкой является узел 4.
Пусть единичная сила перемещается справа от разрезанной панели между 4 и 12 узлами. Рассмотрим равновесие левой части фермы.
S m 4= 0, RА ∙2 d + N 35∙ r 1= 0. (r 1 = h cosa1)
тогда уравнение правой ветви примет вид линии влияния реакции Ra, умноженной на множитель 2 d / r 1:
л. в. N 35 =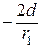 
(л. в. RА) = 
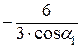(л. в. RА) = - 
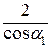(л. в. RА).
Для построения правой ветви линии влияния N 35 отложим на левой опорной вертикали ординату 1∙2/cosa1. Поскольку линия влияния имеет знак минус, указанную ординату откладываем вниз. Правая ветвь будет проходить от 12 до 4 узла.
Р =1 находится слева от разрезанной панели между 1 и 2 узлами. Рассмотрим равновесие правой части фермы.
S m 4= 0, RВ ∙4 d + N 35∙ r 1= 0.
По аналогии
л. в. N 35 =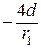 
(л. в. RВ) = 
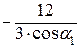(л. в. RА) = 
(л. в. RА).
Откладывая на правой опорной вертикали ординату 1∙4/cosa2, строим левую ветвь линии влияния N 35 от 1 до 2 узла.
Движение единичной силы между 2 и 4 узлами можно осуществить по настилу. В этом случае будет иметь место узловая передача нагрузки, а линия влияния будет очерчена передаточной прямой (пунктирной линией), соединяющей левую и правую ветви. Отметим, что левая и правая ветви пересекаются под моментной точкой. Это свойство линий влияния можно использовать для проверки.
Построим, используя приведенную выше методику, линию влияния усилия N 34. Моментная точка для этого усилия находится в точке «к», в точке пересечения продолжения стержней 2-4 и 3-5. Из подобия треугольников находим, что а = d = 3 м, плечо у усилия N 34 относительно моментной точки составит r 2 = 3 d∙ sina2.
Р = 1 справа от разрезанной панели.
S m к= 0, RА ∙ а - N 34∙ r 2= 0.
л. в. N 34 = 
(л. в. RА) = 
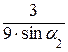(л. в. RА) = 
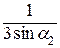(л. в. RА).
Строим правую ветвь, отложив на левой опорной вертикали 1/3sina2. Ординату под 4 узлом (2/9sina2) находим из подобия треугольников.
Р = 1 слева от разрезанной панели.
S m к= 0, RВ ∙7 d + N 34∙ r 2= 0.
л. в. N 34 = 
(л. в. RВ) =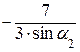 
(л. в. RВ).
Строим левую ветвь, отложив вниз на правой опорной вертикали 7/3sina2. В районе второго узла ордината составит 1/6 от 7/3sina2.
Передаточной прямой соединяем левую и правую ветви. Не трудно убедиться, что они пересекаются под моментной точкой.
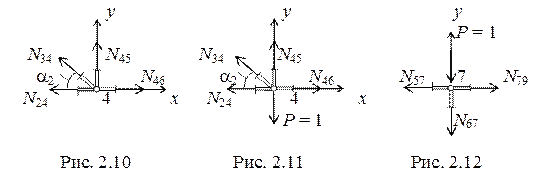
Для определения усилия N 45 и построения его линии влияния можно так же воспользоваться методом моментной точки (точка «к») или методом вырезания узлов. Действительно, вырезав узел 4 (рис. 2.10) можно увидеть что в уравнение S у = 0 входит одно неизвестное N 45. Линия влияния усилия N 34 нами получена. Рассмотрим равновесие 4 узла.
S у = 0. N 34sina2 + N 45 = 0. N 45 = - N 34sina2, или
л. в. N 45 = - (л. в. N 34)∙sina2
Вырезая узел 4, нам пришлось разрезать вторую и четвертую панели, т. е. левая ветвь линии влияния проходит от 1 до 2 узла, а правая от 6 до 12 узла. Строим эти ветви.
В качестве промежуточного будет положение единичной силы в 4 узле (рис. 2.11). В этом случае
S у = 0. N 34sina2 + N 45 – Р = 0. N 45 = - N 34sina2 + 1 = - 
sina2 + 1 = 
.
Откладываем в районе 4 узла 7/9 и проводим две передаточные прямые. Получили линию влияния N 45. Необходимо обратить внимание где пересекаются левая и правая ветви линии влияния N 45.
При езде понизу усилие в стержне 6-7 равно нулю – стержень 6-7 нулевой. В то же время, при езде поверху при движении единичной силы между 5 и 9 узлами в стойке 6-7 будет возникать нагрузка. При движении по остальной части верхнего пояса стержень 6-7 остается нулевым, следовательно левая (от 1 до 5 узла) и правая (от 9 до 12 узла) ветви линии влияния усилия N 67 тоже нулевые. Воспользуемся методом вырезания узлов, когда сила Р = 1 находится в 7 узле (рис. 2. 12).
S у = 0. – N 67 – Р = 0.. N 67 = – 1.
Откладываем ординату «– 1» от проекции 7 узла, проводим передаточные прямые и получаем линию влияния N 67 (см. рис. 2.9).
3 Трехшарнирные арки
Арочными называются системы криволинейного или ломаного очертания, в опорах которых от вертикальной нагрузки возникают наклонные реакции, направленные, как правило, внутрь пролета. Горизонтальная составляющая такой наклонной реакции называется распором. Арочные системы в сравнении с балочными оказываются экономически более выгодными за счет меньших, чем в балках, изгибающих моментов.
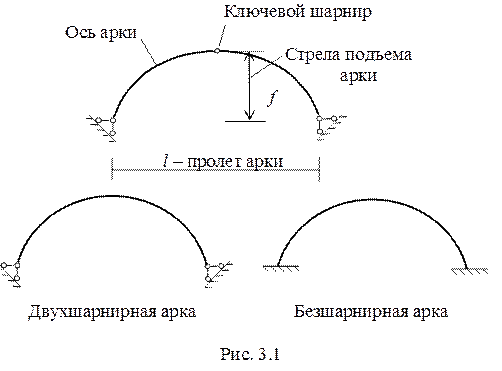
Двухшарнирные и безшарнирные арки являются статически неопределимыми и будут рассматриваться в соответствующем разделе.
Трехшарнирная арка является системой геометрически неизменяемой и статически определимой. Принятые обозначения в арках показаны на рис. 3.1.
В практике встречаются различные по форме и виду арки. В том случае, когда каждая половина трехшарнирной арки представляет собой сплошной брус криволинейного очертания, ее называют аркой со сплошной стенкой (рис. 3.1). При ломаном очертании оси сооружение обычно называют трехшарнирной рамой (рис. 3.2, а, б). Система, изображенная на рис. 3.2, в, носит название трехшарнирной арки с затяжкой.
В практике встречаются арки, образованные из двух ферм, соединенных между собой общим шарниром (рис. 3.2, г). Такие системы называются трехшарнирными фермами.
