ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Рязанский институт (филиал)
Государственного образовательного учреждения
Высшего профессионального образования
«Московский государственный открытый университет»
В. А. Долгоруков, Г. С. Нечипорук
Статически определимые
Стержневые системы
В примерах
Методические указания для
Студентов строительных специальностей
Рязань
ББК 38.112
УДК 624.04
Р 24
В. А. Долгоруков, Г. С. Нечипорук.
Статически определимые стержневые системы в примерах. Методические указания для студентов строительных специальностей. Рязанский институт (филиал) Государственного образовательного учреждения «Московский государственный открытый университет», 2010
В методических указаниях даны необходимые сведения о методах расчета статически определимых стержневых систем (многопролетных балок, ферм, арок и рам) на неподвижную и подвижную нагрузки и приведены примеры по определению внутренних усилий и перемещений. Даны схемы и исходные данные для выполнения расчетно-графических работ.
Печатается по решению методического совета вуза
© Рязанский институт (филиал) МГОУ, 2010
Оглавление
1.Статически определимые многопролетные балки………………………………4
1.1. Общая теория линий влияния…………………………………………………..4
1.2. Расчет статически определимых многопролетных балок на
неподвижную и подвижную нагрузки……………………………………….…...13
2. Статически определимые фермы……….……..………………..…………..….25
2.1. Расчет простейших ферм на неподвижную нагрузку……………………….26
2.2. Расчет ферм на подвижную нагрузку…………………………………….…..32
3. Статически определимые арки…….. ……………………………………….....36
Аналитический расчет трехшарнирной арки………………………………...37
3.2 Расчет арок на подвижную нагрузку………………………………………… 47
4. Расчет на прочность и жесткость ломаных стержней…………… …………...57
4.1 Построение эпюр внутренних усилий в раме………………………………...57
Определение перемещений в стержневых системах методом Мора………61
5.Список рекомендуемой литературы…...……………………….……………….73
Приложения ………………………………..…………………………………….....74
Задание к расчетно-графической работе № 1 (многопролетная балка)………..75
Задание к расчетно-графической работе № 2 (статически определимая ферма)77
Задание к расчетно-графической работе № 3 (трехшарнирная арка, рама)……81
Задание к контрольной работе (статически определимая рама)……………..….85
Статически определимые многопролетные балки
Общая теории линий влияния
Понятие о линиях влияния
При расчете мостов, кранов и других инженерных сооружений часто приходится иметь дело с подвижной нагрузкой различного вида. Обычно подвижная нагрузка состоит из системы параллельных друг другу (чаще вертикальных) грузов, между которыми сохраняется неизменное положение. Примерами такой нагрузки являются поезд, перемещающийся по железнодорожному мосту, кран, движущийся по подкрановой балке, и др.
Усилия в том или ином элементе сооружения (а также его деформации) зависят от положения подвижной нагрузки. Для определения расчетных величин усилий необходимо из всех возможных положений нагрузки выбрать такое, при котором рассчитываемый элемент будет находиться в наиболее неблагоприятных условиях. Такое положение нагрузки называется невыгоднейшим, или опасным.
Указанные выше задачи позволяют решать линии влияния (л. в.). Линия влияния это график, выражающий изменение той или иной величины (опорной реакции, внутреннего усилия, перемещения в заданном сечении и т. п.) от положения движущегося по сооружению единичного груза постоянного направления.

|
На рис. 1. 1 для примера показана линия влияния прогиба в сечении «с» при перемещении силы Р = 1 по сооружению.
Линию влияния необходимо отличать от эпюры. Это противоположные друг другу понятия. Действительно, ординаты эпюры характеризуют распределение изучаемого фактора (например изгибающего момента) по различным сечениям балки при неподвижной нагрузке; ординаты линии влияния, наоборот, характеризуют изменение фактора (например того же момента), возникающего в одном определенном сечении при перемещающейся по длине балки силы Р = 1.
Зная линию влияния какой-либо искомой величины нетрудно определить ее значение при действии системы сосредоточенных грузов, распределенной нагрузки или сосредоточенного момента.

|
а) Влияние системы сосредоточенных грузов (рис. 1. 2). Пусть имеем систему сосредоточенных грузов Р 1, Р 2,…. Рn. Требуется определить влияние этой нагрузки на величину Z, для которой известна линия влияния. Влияние каждой из сил выражается произведением Pi∙yi. Пользуясь принципом независимости действия сил можем записать
Z = P 1 ∙y 1 + P 2 ∙y 2 +……+ Pn∙yn = 
б) Влияние сосредоточенного момента M (рис. 1. 3). Любой момент можно заменить парой сил, расположенных на плече h. Тогда его влияние можно оценить по следующей формуле
Z = M (y лев – y пр)/ h., или Z = M∙ tgφ,
где φ – угол наклона касательной к линии влияния Z в точке приложения М.

|
в) Влияние распределенной нагрузки (рис. 1. 3). Элементарная сила q ∙ dx будет вызывать элементарное усилие dZ = q ∙ dx ∙ y. Тогда полное усилие Z определится как

В случае равномерной нагрузки при q = const

где ω – площадь линии влияния Z под распределенной нагрузкой q.
Построение линий влияния в простой балке
Построение линий влияния опорных реакций.

|
Для построения линии влияния какого-либо параметра необходимо получить формулу (выражение) этого параметра.
Запишем выражение для реакции Ra
S MB = 0. RAl – P (l – x) = 0.
 или
или
л. в.  . (1.1)
. (1.1)
при х = 0 Ra = 1, при х = l Ra = 0.
Линия влияния реакции Ra показана на рис. 1.4.
Для построения л.в. RВ запишем выражение этой реакции.
S MА = 0. RВl – P∙ x = 0.  или
или
л. в.  . (1.2)
. (1.2)
При х = 0 RВ = 0, при х = l RВ = 1. Линия влияния реакции RВ показана на рис. 1.4.
Построение линий влияния внутренних усилий.
Построение линий влияния Qc.
Пусть единичная сила находится справа от сечения «с» (рис. 1.5). Тогда, рассматривая левую от сечения часть балки, можем записать Qc = Ra, или
л. в. Qc = л. в. Ra, (1.3)
получили уравнение правой ветви л. в. Qc,то есть, когда Р = 1 перемещается по балке на отрезке с - В линия влияния поперечной силы повторяет линию влияния реакции RА.

|
Теперь Р = 1 перемещается слева от сечения «с». Рассмотрим правую часть балки.
Qc = - Rв, или
л. в. Qc = (- 1)л. в. RВ. 1.4)
Получили уравнение левой ветви. В соответствии с полученными уравнениями (1.3) и (1.4) строим линию влияния Qc (рис. 1.5).
Для построения линии влияния изгибающего момента в сечении «С» используем ту же методику, что и при построении л. в. Qc.
Пусть Р = 1 перемещается справа от сечения «С». Рассмотрим левую часть балки. Изгибающий момент в сечении «С» будет
Мc = Ra∙а, или
л. в. Мc = (л. в. Ra) ∙а, (1.5)
Таким образом, правая ветвь линии влияния повторяет линию влияния Ra, с множителем «а» (рис. 1.5).
Теперь Р = 1 перемещается слева от сечения «С». Рассмотрим правую часть балки, тогда
Мc = RВ∙b, или
л. в. Мc = (л. в. RB) ∙b, (1.6)
при х = 0 RВ = 0, Мc = 0, при х = а Мc = (л. в. RB) ∙b = (х /l)∙ b = a∙b / l.
Линия влияния Мc приведена на рис. 1.5.
Отметим, что при построении линий влияния положительные ординаты откладывают выше оси ординат. Линии влияния реакций и поперечных сил безразмерны, поскольку величина единичной силы безразмерна, линии влияния моментов имеют размерность «метр».
Линии влияния для консольной балки

|
Линия влияния реакции Ra
Из уравнения равновесия S y = 0, получим Ra = P = 1, т. е.
л. в. RB = 1 (см. рис. 1.6 (б)).
Линия влияния поперечной силы в сечении «k» Qk.
Единичная сила Р = 1 находится справа от сечения «k». Рассмотрим правую часть балки.
Qk = P = 1.
Далее, Р = 1 слева от сечения «k». Рассмотрим опять правую ненагруженную часть балки.
Qk = 0.
Линия влияния изгибающего момента в сечении «k» Мk.
Пусть Р = 1 справа от сечения «k». Рассмотрим правую часть балки.
Мk = P∙х.
При х = 0, Мk = 0, при х = а, Мk = 1∙ а = а.
Теперь Р = 1 слева от сечения «k». Рассмотрим опять правую ненагруженную часть балки.
Мk = 0.
Линии влияния Qk и Мk приведены на рис. 1. 6 (в, г).
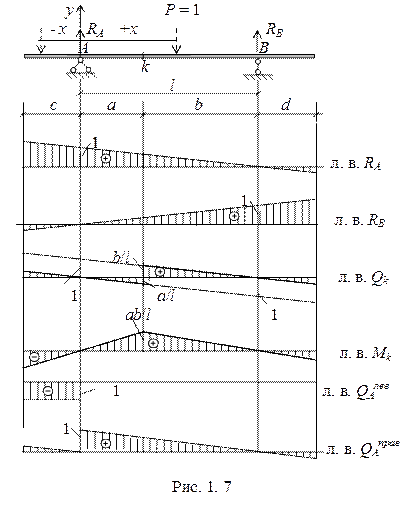
Пример 1.1. Построить линии влияния реакций и Qk и Мk в шарнирно опертой балке с консолями (рис. 1.7.).
Решение. Если выбрать начало координат на левой опоре в точке А, то полученные выше выражения для линий влияния в простой балке справедливы и в данном случае. При этом, координата х будет меняться от – с до l + d.
Дополнительно необходимо построить линии влияния поперечной силы для двух соседних сечений – одно слева от опоры А, другое справа от той же опоры.