Определение опорных реакций

|
При действии внешней нагрузки на трехшарнирную арку (рис. 3.3) в каждой ее опоре возникает по две реакции. Всего, таким образом, имеется четыре неизвестные реакции – две вертикальные RA, RB и две горизонтальные НA и НB. Для расчета трехшарнирной арки кроме трех уравнений равновесия, которые дает статика для системы сил, расположенной в одной плоскости, можно составить четвертое уравнение, основанное на том, что сумма моментов всех сил, приложенных по одну сторону от ключевого шарнира С, равна нулю. Действительно, это уравнение для изгибающего момента в поперечном сечении, а в шарнире момент отсутствует.
Для трехшарнирной арки (рис. 3.3) при определении реакций будут записаны следующие уравнения:
S mB = 0, - RAl + P 1(l – a 1) + P 2 a 2 = 0, (а)
RA = [ P 1(l – a 1) + P 2 a 2]/ l.
S mA = 0, RBl – P 1 a 1 – P 2(l – a 2) = 0, (б)
RB = [ P 1 a 1 + P 2(l – a 2)]/ l.
Уравнения (а) и (б) для вычисления вертикальных реакций имеют тот же вид, что и уравнения в балочной системе. Для вычисления распора запишем следующие уравнения:
S x = 0, HA – HB = 0, HA = HB = H.
S mC пр = 0, RBl 2 – P 2(l 2 – a 2) – HBf = 0, (в)
HB = H = [ RBl 2 – P 2(l 2 – a 2)]/ f, или:
 (3.1)
(3.1)
В выражении (3.1) МС бал представляет собой изгибающий момент в сечении С в балке, перекрывающей тот же пролет и воспринимающей заданную на трехшарнирную арку вертикальную нагрузку (рис. 3.3). Из формулы (3.1) следует, что величина распора Н обратно пропорциональна стреле подъема арки f.
Определение внутренних усилий в арке
от вертикальной нагрузки
При действии на арку только вертикальных нагрузок (рис. 3.4, а) изгибающий момент в сечении с абсциссой х равен:
Mx = RAx – P 1(x - a 1) – P 2(x - a 2) – Hy,
или:
Мx = Mx бал - H ∙ y, (3.2)
где Мх бал — изгибающий момент в балке (рис. 3.4, б) от той же нагрузки в сечении с абсциссой х (так называемый балочный момент). Формулой (3.2) удобно пользоваться при построении эпюры моментов в арке. Значения Мх бал непосредственно берут из эпюры моментов, построенной для балки. Величину распора находят по формуле (3.1).
Полученная формула для Мх наглядно показывает уменьшение изгибающего момента в арке по сравнению с балкой, что подтверждает экономичность арочной конструкции по сравнению с балочной. Это видно из построений на рис. 3.4, г, где показано совмещение балочной эпюры моментов и кривой, соответствующей слагаемому Н∙у в формуле (3.1). На рис. 3.4, д показан вид эпюры моментов Мх в арке.

Аналогичные формулы можно получить для поперечной Qx и продольной Nx сил. Для этого спроецируем все приложенные слева от сечения n – n силы (рис. 3. 4, в) сначала на нормаль к оси арки в сечении с абсциссой х, а затем на касательную к ней:
Qx = (RA – P 1 – P 2)cosj x – H sinj x,
Nx = + (RA – P 1 – P 2)sinj x + H cosj x.
Нетрудно убедиться, что величина, стоящая в круглых скобках в записанных выше выражениях, представляет собой величину поперечной силы в балке в сечении с той же абсциссой х; тогда эти формулы примут вид:
Qx = Qx бал cosj x - Н sinj x, (3.3)
Nx = Qx бал sinj x + H cosj x. (3.4)
Отметим, что в арке принято считать N > 0 при сжатии.
Рациональная ось арки
Из формулы (3.2) следует, что в том случае, когда очертание оси арки совпадает с очертаниями балочной эпюры моментов М бал, называемой кривой давления, т. е. если
 (3.5)
(3.5)

то в такой арке изгибающий момент Мх = 0.
Уравнение (3.5) называют уравнением рациональной оси арки. На рис. 3. 5, в приведены очертания арок с рациональной осью для различных случаев нагружения.
Пример 3.1 Для заданной трехшарнирной арки с размерами, показанными на рис. 3. 6, вычислить значения внутренних усилий в сечениях m и n. Построить эпюры внутренних усилий. Уравнение оси арки – квадратная парабола с началом координат в точке А:
 , где l = 12 м, f = 4 м.
, где l = 12 м, f = 4 м.
Решение.
1. Определяем опорные реакции:
S mA = q 6×3 + P∙ 9 – RB 12 = 0. RB = 6 кН.
S mB = q 6×9 + P∙ 3 – RA 12 = 0. RA = 10 кН.
H = MC бал/ f = (RB 6 – P∙ 3)/4 = 6 кН.
2. Строим эпюры Qх бал и Мх бал.
3. По формуле (3.2) вычисляем значения Мх, получив предварительно ординаты заданных сечений m и n:

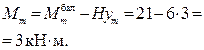

4. Вычисляем Qm и Qn, используя формулу (3.3)
Qm=Qm балcosj m - H sinj m
Для вычисления тригонометрических функций воспользуемся следующими математическими соотношениями:

|
 ;
;

 ,
,
тогда
 ,
, 
 ,
,
 ,
,  .
.
Аналогично:
sinj n = - 0,555, cosj n = 0,832.
Подсчитаем значения Q в заданных сечениях:
Qm = Qm балcosj m - H sinj m = 4×0,832 – 6×0,555 = 0.
В сечении n эпюра Q бал имеет разрыв, аналогично будет разрыв и в эпюре поперечных сил арки. Поэтому необходимо подсчитать поперечную силу слева и справа от сечения:

Одновременно найдем поперечные силы в опорных сечениях А и В.



QA = 10×0,6 – 6×0,8 = 1,2 кН; QB = -6×0,6–6(-0,8) = 1,2 кН.
QC = - 2×1 = - 2 кН.
5. Вычисляем продольные усилия по формуле (3.4):
Nm = Qm балsinj m + H cosj m = 4×0,555 + 6×0,832 = 7,218 кН,
Nn л = (-2)×(- 0,555) + 6×0,832 = 6,108 кН,
Nn пр = (- 6)×(- 0,555) + 6×0,832 = 8,328кН,
В опорных сечениях:
NA = 10×0,8 + 6×0,6 = 11,6 кН,
NВ = (-6)×(-0,8) + 6×0,6 = 8,4 кН.
Таблица 1.
| № сеч. | х (м) | y (м) | tg φ | sinφ | cosφ | M б | Н | М | Q б | Q б∙ cosφ | H ∙ sinφ | Q | Q б∙ sinφ | H ∙ cos φ | N |
| A | 1.333 | 0.8 | 0.6 | 4.8 | 1.2 | 3.6 | 11.6 | ||||||||
| m | 0.667 | 0.555 | 0.83 | 3.33 | 3.33 | 2.22 | 4.99 | 7.22 | |||||||
| C | -2 | -2 | -2 | ||||||||||||
| n (л) | -0.667 | -0.555 | 0.83 | -2 | -1.66 | -3.33 | 1.66 | -1.11 | 4.99 | 6.11 | |||||
| n( пр) | -0.667 | -0.555 | 0.83 | -6 | -4.99 | -3.33 | -1.69 | -3.33 | 4.99 | 8.33 | |||||
| B | -1.333 | -0.8 | 0.6 | -6 | -3.6 | -4.8 | 1.2 | 4.8 | 3.6 | 8.4 |
6. Сводим полученные значения в таблицу 1 и строим эпюры внутренних усилий в арке (рис. 3. 6).
Пример 3.2
Для заданной трехшарнирной рамы с размерами и нагрузкой, показанными на рис. 3. 7, а, построить эпюры внутренних усилий.
Решение.
1. Определяем опорные реакции:
S mA = - q 12×18 - P∙ 3 + RB 24 = 0. RВ = 10,25 кН.
S mB = q 12×6 + P∙ 21 – RA 24 = 0. RА = 11,75 кН.
H = MC бал/ f = (RА ∙12 – P∙ 9)/6 = 8.5 кН.
2. Строим эпюры Qх бал и Мх бал (рис. 3. 7, б).
3. По формулам (3.2), (3.3), (3.4) вычисляем значения внутренних усилий, используя табличную форму.
 (3.2)
(3.2)
Qk=Qk балcosj k - H sinj k (3.3)
Nk = Qk балsinj k + H cosj k (3.4)
В таблицу 2 заносим опорные точки А и В, точки приложения сосредоточенной силы, начала и конца распределенной нагрузки и узлы рамы m и n. В точках приложения сосредоточенных сил в узлах необходимо находить по два усилия (слева и справа от сечения), поскольку в точках приложения сосредоточенных сил скачкообразно меняется поперечная сила, а в узлах слева и справа различный угол наклона поперечного сечения.

|
Таблица 2.
| № сеч. | х (м) | y (м) | sin φ | cos φ | M б | Н | М | Q б | Q б cosφ | H sinφ | Q | Q б sinφ | H cos φ | N |
| A | 0.707 | 0.707 | 8.5 | 11.75 | 8.31 | 6.01 | 2.3 | 8.31 | 6.01 | 14.32 | ||||
| k( л ) | 0.707 | 0.707 | 31.25 | 8.5 | 5.7 | 11.75 | 8.31 | 6.01 | 2.3 | 8.31 | 6.01 | 14.32 | ||
| k( пр ) | 0.707 | 0.707 | 31.25 | 8.5 | 5.7 | 1.75 | 1.24 | 6.01 | -4.77 | 1.24 | 6.01 | 7.25 | ||
| n( л ) | 0.707 | 0.707 | 40.5 | 8.5 | -10.5 | 1.75 | 1.75 | 6.01 | -4.77 | 1.24 | 6.01 | 7.25 | ||
| n( пр ) | 40.5 | 8.5 | -10.5 | 1.75 | 1.75 | 1.75 | 8.5 | 8.5 | ||||||
| C | 8.5 | 1.75 | 1.75 | 1.75 | 8.5 | 8.5 | ||||||||
| m (л) | 46.5 | 8.5 | -4.5 | -4.25 | -4.25 | -3.33 | -0.92 | 8.5 | 8.5 | |||||
| m( пр) | -0.707 | 0.707 | 46.5 | 8.5 | -4.5 | -4.25 | -3.0 | -6.01 | 3.01 | 3.0 | 6.01 | 9.01 | ||
| B | -0.707 | 0.707 | 8.5 | -10.2 | -7.25 | -6.01 | -1.24 | 7.25 | 6.01 | 13.3 |
Используя данные 8, 12 и 15 столбцов таблицы 2 строим эпюры внутренних усилий в трехшарнирной раме (рис. 3.8).







