Интеграл Дюамеля и интеграл наложения

Интеграл Дюамеля может быть получен, если аппроксимировать приложенное на входе цепи воздействие f ₁(t) с помощью совокупности единичных функций, сдвинутых друг относительно друга на время, равное (рис.13.7).

Реакция цепи f ₂(t) на каждое ступенчатое воздействие определится как

…………………………..

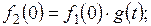
Результирующую реакцию цепи на систему ступенчатых воздействий найдем по принципу наложения:

где п – число аппроксимирующих участков, на которые разбит интервал времени от 0 до t.

Умножим и разделим выражение под знаком суммы на и перейдем к пределу с учетом того, что при →0 k → τ, получим первую форму интеграла Дюамеля

или

Вторая форма имеет вид

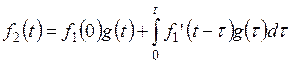Третья и четвертая формы имеют вид:

;

При нахождении реакции цепи с помощью интеграла наложения используется импульсная характеристика h (t). Для получения общего выражения интеграла наложения аппроксимируем входной сигнал f ₁(t) с помощью системы единичных импульсов длительностью dτ c амплитудой f ₁(τ) и площадью f ₁(τ) dτ (рис. 13.8).

Выходная реакция цепи на каждый из единичных импульсов

Используя принцип наложения, получим суммарную реакцию цепи на систему единичных импульсов:

Электронные модели цепей

Широкое применение в устройствах импульсной и вычислительной техники находят интегрирующие и дифференцирующие цепи. Они применяются для формирования линейно изменяющихся напряжений и токов, селекции сигналов, линейного преобразования различных импульсов.

Простейшие интегрирующие и дифференцирующие цепи могут быть реализованы, например, на базе RC -цепочки.

Интегрирующей называется цепь, в которой напряжение на выходе цепи пропорционально интегралу входного напряжения. Эта цепь описывается уравнением

Рассмотрим интегрирующую цепь (рис 13.2).

Здесь входное напряжение подается на RC – цепочку, а выходное снимается с емкости.

Эта цепь будет интегрирующей в том случае, если сопротивление резистивного элемента значительно превышает сопротивление емкостного . То есть параметры этой схемы таковы, что , где t_u – длительность входного сигнала.

Согласно второму закону Кирхгофа

. (13.3)

Поскольку , то и , тогда напряжением на емкости и_С можно пренебречь и считать, что все входное напряжение приложено к резистору . В этом случае ток в цепи можно определить по закону Ома:

Наряжение на емкости связано с током соотношением

Подставив сюда выражение для тока, получим

Дифференцирующей называют такую цепь, напряжение на выходе которой пропорционалино производной от входного напряжения. Эта цепь описывается уравнением

Рассмотрим дифференцирующую цепь (рис. 13.3).

Здесь входное напряжение подается на RC -цепочку, а выходное снимается с резистора.

Эта цепь будет дифференцирующей в том случае, если сопротивление емкостного элемента значительно превышает сопротивление резистивного . То есть параметры этой схемы таковы, что .