После замыкания ключа емкость начинает заряжаться и по цепи будет протекать ток, который уменьшается по мере того, как емкость заряжается.
Рассмотрим схему цепи, содержащей емкость и резистивный элемент (рис. 11.6) и подключаемой к источнику постоянного напряжения.
Составим для данной схемы уравнение по второму закону Кирхгофа для независимой переменной иС:
.
Решаем это уравнение классическим методом.
Решение ищем в виде суммы свободной и принужденной составляющих
.
 |
Принужденную составляющую определяем в установившемся режиме. Исходя из закона Ома, напряжение на резистивном элементе можно определить по формуле
.
В свою очередь ток определяем из закона Ома для полной цепи:
.
Поскольку частота постоянного тока равна нулю, то емкостное сопротивление будет бесконечно большим и ток установившегося режима становится равным нулю I = 0.
Следовательно, падения напряжения на резисторе не будет, и согласно второму закону Кирхгофа все напряжение будет приложено к емкости:
.
Для определения свободной составляющей запишем характеристическое уравнение. Рассмотрим два способа, используя которые можно составить характеристическое уравнение.
1. Заменим в дифференциальном уравнении
символ дифференцирования 
и приравняем нулю источники U = 0, получим
, откуда 
.
2. Запишем выражение для комплексного сопротивления цепи и приравниваем его нулю
.
Сделаем замену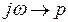 
, тогда 
или 
.
Решение для свободной составляющей записываем в виде
.
Полное напряжение запишется
.
Постоянную интегрирования А находим, исходя из законов коммутации и независимых начальных условий.
В первый момент переходного режима t = 0 напряжение на емкости остается таким же, каким было в последний момент предшествующего установившегося режима, а до включения цепи оно было равно нулю, следовательно,
.
Подставляем в выражение для напряжения значение при t = 0
, отсюда 
.
Окончательно выражение для напряжения на емкости запишется
.
Здесь 
– постоянная времени переходного процесса.
График переходного процесса представлен на рис. 11.7.
 |
Найдем закон изменения емкостного тока.
Известно, что ток, протекающий в емкости выражается следующей формулой: 
.
Подставим сюда выражение для напряжения и продифференцируем
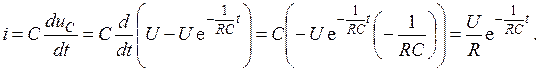
Таким образом, в первый момент переходного процесса t = 0 емкостный ток скачком увеличивается до максимального значения U/R, а затем экспоненциально уменьшается до нуля.
Отключение емкости, заряженной до напряжения иС = U, выполняют с одновременным замыканием ее накоротко (рис. 11.8).
 |
В момент коммутации ток меняет направление на противоположное и конденсатор начинает разряжаться, рассеивая накопленную энергию на резистивном элементе. Следовательно, по мере разрядки конденсатора ток будет уменьшаться, а принужденная составляющая напряжения на емкости стремиться к нулю.
Дифференциальное уравнение для этой цепи имеет вид
.
Составим характеристическое уравнение, заменяя в дифференциальном уравнении символ дифференцирования 
:
, откуда 
.
Решение для свободной составляющей ищем в виде
.
Поскольку принужденная составляющая равна нулю, то полное напряжение на емкости опишется этим же уравнением:
.
Постоянную интегрирования А находим, исходя из законов коммутации и независимых начальных условий.
В первый момент переходного режима t = 0 напряжение на емкости остается таким же, каким было в последний момент предшествующего установившегося режима, а до выключения цепи оно было равно U, следовательно,
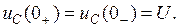
Подставляем в выражение для напряжения значение при t = 0, получим
.
Окончательно выражение для напряжения на емкости запишется
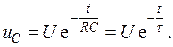
Разрядный ток равен
 |
.
Изменение напряжения и тока при отключении емкости представлено на рис. 11.9.
