Для анализа электрических цепей, в которых действуют непериодические сигналы, используют спектральные представления, базирующиеся на паре преобразований Фурье, которые могут быть получены путем предельного перехода от ряда Фурье в комплексной форме.
Пусть имеется некоторый непериодический сигнал f (t), удовлетворяющий условию абсолютной интегрируемости в бесконечных пределах
.
С физической точки зрения это означает, что задается реализуемый сигнал с конечной энергией, при этом
,
то есть модуль сигнала f (t) имеет ограниченный показатель роста.
Мысленно превратим этот сигнал в периодический путем его повторения через определенный промежуток времени, который будем считать периодом Т (рис. 13.1).
К полученному таким образом сигналу можно применить разложение Фурье в комплексной форме
,
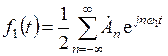где обозначили:
; 
.
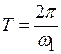Подставим 
в предыдущее уравнение
.
Перейдем в этом выражении к пределу, учитывая, что при Т→∞ 
; 
.
.
Внутренний интеграл
(13.1)
называется спектром сигнала.
С учетом спектра сигнала исходный сигнал можно записать
. (13.2)
Уравнение (13.1) называют прямым преобразованием Фурье; уравнение (13.2) – обратным преобразованием Фурье.
Поскольку спектр сигнала F (jω) – комплексная функция частоты, то он может быть записан в алгебраической и показательной формах:
где
; 
Здесь
– амплитудный спектр сигнала;
– фазовый спектр сигнала.
– спектральная плотность энергии сигнала.
Между спектрами периодического и непериодического сигналов существует следующая связь:
.
В отличие от линейчатого спектра периодических сигналов, спектр непериодических сигналов носит сплошной характер (разница соседних частот равна dω).
Сигналы f (t) и спектры F (jω) обладают рядом свойств:
1) свойство линейности
,
где аk – коэффициенты разложения;
2) дифференцирование сигнала соответствует умножению его спектра на величину jω:
;
3) интегрирование сигнала соответствует делению его спектра на jω:
;
4) смещение сигнала во времени на величину τ:
;
5) умножение спектров (теорема свертки):
;
6) изменение масштаба независимого переменного:
.
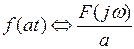Из всего вышеизложенного в данной главе следует, что периодический несинусоидальный и непериодический сигналы могут быть представлены суперпозицией гармонических составляющих.
Расчет цепей при непериодических воздействиях
Временным методом
При расчете электрических цепей, в которых действуют непериодические токи и напряжения, могут использоваться временной и частотный методы анализа. Частотный метод мы рассмотрели, теперь остановимся на временном методе.
В основе временного метода лежат понятия переходной и импульсной характеристик цепи.
Переходной характеристикой g (t) называют реакцию цепи на воздействие в форме единичной функции 1(t) (рис. 13.4).
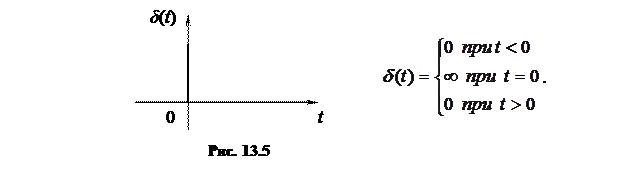Импульсной характеристикой h (t) называют реакциию цепи на воздействие в виде единичной импульсной функции δ (t) (δ -функции), изображенной на рис. 13.5.
 |
По своей сути эта функция является физически нереализуемой математической абстракцией, но она обладает рядом интересных свойств и широко используется в теоретических исследованиях. Формально она представляет собой математическую идеализацию единичного импульса, площадь которого равна единице при длительности импульса τ и высоте 1/ τ при τ→ 0 (рис. 13.6).
В зависимости от типа реакции (ток или напряжение) различают переходные и импульсные характеристики по току и напряжению:
gi (t); gu (t); hi (t); hu (t).
Использование переходной и импульсной характеристик позволяет свести расчет реакции цепи от воздействия сигнала произвольной формы к определению реакции цепи на простейшее воздействие в виде единичной 1(t) или импульсной δ (t) функции, с помощью которых можно аппроксимировать исходный сигнал.
Между переходной и импульсной характеристиками существует определенная связь, которую можно установить, если представить единичную импульсную функцию через предельный переход разности двух единичных функций величиной 1/ τ, сдвинутых друг относительно друга на время τ:
,
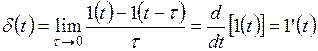то есть δ (t) функция равна производной от единичной функции.
В линейных цепях это соотношение сохраняется и для импульсных и переходных характеристик:
.
Это уравнение справедливо для цепи с нулевыми начальными условиями g (0) = 0. Для ненулевых начальных условий g (0) ≠ 0 g (t) представляют в виде
где g 1(0) = 0. Тогда уравнение связи запишется следующим образом:
.
Для нахождения переходных и импульсных характеристик цепи можно использовать классический и операторный методы расчета переходных процессов, считая, что цепь подключается к источнику с единичным напряжением.
Если переходная или импульсная характеристики известны, то реакция цепи на воздействие произвольной формы может быть найдена с помощью интеграла Дюамеля, либо интеграла наложения.
