Пусть на входе цепи (рис. 11.10) действует постоянное напряжение U.
Запишем уравнение состояния цепи
.
Будем выполнять расчеты для напряжения емкости. Учтем, что емкостный ток можно определить по формуле
.
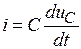Подставим ток в дифференциальное уравнение, учитывая то, что ток через все элементы протекает один и тот же
.
Решение ищем в виде суммы свободной и принужденной составляющих.
.
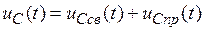Находим принужденную составляющую.
Поскольку сопротивление емкости постоянному току бесконечно велико, то принужденная составляющая тока будет равна нулю iпр = 0. Падение напряжения на резистивном элементе также будет равно нулю, а индуктивность представляет собой короткое замыкание для постоянного тока, то есть UL = 0, следовательно, все напряжение источника в установившемся режиме будет приложено к емкости иСпр = U.
Для определения свободной составляющей составляем характеристическое уравнение, приравнивая нулю источники и заменяя символ дифференцирования оператором р
→ 
.
Находим корни уравнения
.
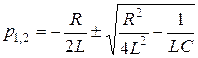Рассмотрим решение для двух случаев корней.
Апериодический процесс
Решение для свободной составляющей ищем в виде
,
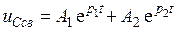тогда
.
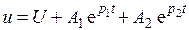Для определения постоянных интегрирования записываем первую производную от напряжения
.
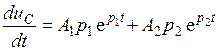Находим в начальный момент переходного процесса t = 0 значения напряжения на емкости uC (0) и его производной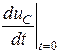 
.
По второму закону коммутации 
, следовательно, uC (0) = 0.
Первую производную находим из выражения для тока
.
По первому закону коммутации i (0+) = i (0-) = 0. Так как С ≠ 0, то нулю равна производная
.
Запишем уравнения для напряжения и его производной при t = 0
;
,
Из первого уравнения находим
,
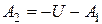Подставляем во второе уравнение
.
Отсюда получаем:
; 
.
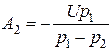Запишем окончательное решение для напряжения
;
 |
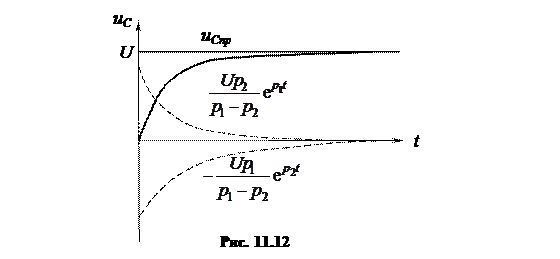График переходного процесса для напряжения с учетом того, что
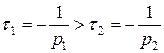показан на рис. 11.12.
Найдем выражение для тока. Для этого необходимо продифференцировать выражение для напряжения
.
 |
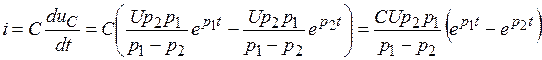График переходного процесса для тока показан на рис. 11.13.
2. Колебательный процесс
В этом случае корни характеристического уравнения будут комплексно-сопряженные
.
Постоянные времени переходного процесса определятся выражением
Принужденные составляющие тока и напряжения имеют те же значения, что и в предыдущем случае
Начальные условия:
.
Поскольку корни комплексно-сопряженные, решение для свободной составляющей ищем в виде
.
Запишем уравнения для напряжения и его производной:
.
Используя начальные условия, получаем
.
Из первого уравнения находим
.
Подставляем во второе
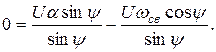
Отсюда
.
Запишем решение для напряжения
.
 |
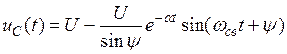График переходного процесса будет иметь вид (рис. 11.14).
Найдем ток в цепи
.
Приведем это выражение к привычному виду. Умножим и разделим выражение в скобках на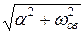 
.
.
Учтем, что
.
Рассмотрим выражение для корней характеристического уравнения
.
Здесь
; 
.
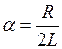Тогда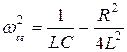 
, отсюда 
,
где ω 0 – резонансная частота.
С учетом этого выражение для тока запишется
.
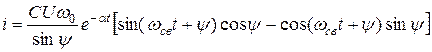По правилам тригонометрических преобразований
.
Если принять, что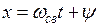 
, а 
, то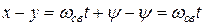 
.
Окончательно получим
.
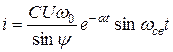Если учесть, что
, а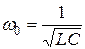 
,
то выражение для тока можно записать в виде
 |
.
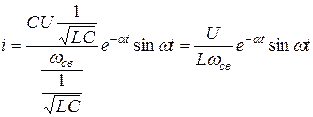График изменения тока показан на рис. 11.15.
Таким образом, переходной процесс будет затухающим. Скорость затухания характеризуется декрементом колебаний, равным отношению двух соседних амплитуд
.
Логарифмический декремент колебаний определится выражением:
.
