Температура оказывает на скорость более сильное влияние, чем концентрации реагирующих веществ. В подавляющем большенстве случав при повышении температуры скорость реакции возрастает. Так, осуществить синтез воды (2Н2 + О2 – 2Н2О) при 200С даже на 15 % практически невозможно. На это потребуется 54 миллиона лет; при 5000С на это потребуется всего 50 минут, а уже при 7000С реакция протекает мгновенно.
Исследование выражения V = К * Сn показывает, что изменение скорость реакции с температурой может быть сопряжено с измене7нием 3-х величин: константы, концентрации и порядка реакции.
Обычно концентрация (особенно для реакций в жидкой фазе) изменяется с температурой мало. Изменение порядка реакции под влиянием температуры – довольно редкое явление.
Вследствие этого в химической кинетике изменение скорости реакции под влиянием температуры в первую очередь связывает с изменением константы скорости реакции. Исторически известны два вида зависимости константы скорости от температуры: эмпирическое правило Вант-Гоффа и более строгое уравнение Аррениуса.
В области умеренных температур для гомогенных и многих гетерогенных реакций справедливо правило Вант-Гоффа: при постоянных концентрациях реагирующих веществ увеличение температуры на 100С (или 10 К) приводит к возрастанию скорости реакции в 2 ÷ 4 раза.
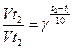или 
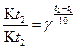(2.11)
Величина γ = 2 – 4, постоянная для данного процесса, называется коэффициентом Вант-Гоффа или температурным коэффициентом. Из выражения (2.11) следует, что скорость возрастает тем сильнее, чем больше для нее коэффициент Вант-Гоффа.
При γ = 2 увеличение температуры на 100 К ведет к росту скорости реакции в 210=1024 раза, а при γ = 3 – в 310 ≈ 60000 раз.
Более строгая зависимость константы скорости от температуры выражается уравнением Аррениуса (1889):
ln K = - 
(2.12)
которое показывает, что логарифм (натуральный и десятичный) константы скорости линейно зависит от обратной абсолютной температуры.
В уравнении (2.12) А и В – эмпирические константы для данной реакции, которые можно определить графическим способом. Для этого в координатах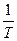 
- ln К строят график по экспериментальным значениям константы скорости изучаемой реакции при различных температурах. Опытные точки в пределах статистического разброса данных находятся на прямой линии
 |
Константа А вычисляется как тангенс угла наклона прямой к оси абсцисс, а постоянная В численно равна отрезку, отсекаемому прямой на оси ординат при
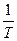= 0
Для объяснения предложенного уравнения Аррениус использовал некоторые теоретические представления о механизме реакций. Как уже было сказано, необходимым условием того, что бы между частицами (атомами, молекулами, ионами) исходных веществ произошло химическое взаимодействие, является их соударение. Но если бы каждое соударение оканчивалось взаимодействием, то все реакции протекали бы со скоростью взрыва; ведь молекулы содержащиеся в 1 см3 газа, испытывают ежесекундно такое колоссальное число соударений, что ему должна отвечать скорость превышающая экспериментальную в сотни и миллиарды раз.
Так, при р = 101,3 кПа и 5000С ежесекундное число столкновений в 1 см3 газа составляет ≈ 1028. Но, этот факт не противоречит закону действующих масс, так как число столкновений приводящих к реакции, пропорционально общему числу. Аррениус высказал гипотезу о том, что в реакцию вступают только молекулы, которые в момент столкновения находятся в активном состоянии, т.е. достигли энергетического уровня, характерного для данной реакции, ее энергетического барьера. Чем больше активных молекул при данных условиях, тем больше скорость реакции.
Активность молекул неразрывно связана с процессом, в котором они участвуют. Вне процесса понятие активности не имеет смысла. Например, одни и те же молекулы водорода при одних и тех же условиях по отношению к реакции Н2 + F2 = 2НF могут быть активными, а по отношению к реакции Н2 + I2 = 2НI неактивными.
Какие же молекулы следует считать активными?
Всякая молекула, обладающая избытком энергии по сравнению со средней энергией и вступающая в реакцию данного типа, называется активной по отношению к этой реакции.
А та избыточная энергия, которой должна обладать молекула, чтобы быть активной по отношению к данному процессу, называется энергией активации этого процесса – Еа. Она измеряется в Дж/моль или кДж/ моль.
Чем больше энергия активации данного процесса, тем меньше будет активных молекул среди общего числа их по отношению к данному процессу, тем меньше будет скорость.
Таким образом, первое необходимое условие химического взаимодействия двух частиц – их столкновение – должно быть дополнено вторым необходимым условием – активным состоянием частиц в момент столкновения. Величина энергии активации есть тот фактор по средством, которого сказывается влияние природы реагирующих веществ на скорость реакции. Другими словами, что бы прореагировать в данной реакции, молекула должна иметь внутреннюю энергию, превышающую некоторую пороговую величину. При этом надо помнить, что ни какой особой формой энергией активации – не существует. Это некоторое избыточное количество внутренней энергии и оно может представлять собой:
а. повышенную кинетическую энергию поступательного движения;
б. повышенную кинетическую энергию вращательного движения;
в. Повышенную энергию колебательного движения атома или атомных групп в молекуле;
г. повышенную энергию электронов в молекуле, атоме или радикале.
С. Аррениус установил, что энергия активации связана с константой А (уравнение 2.12) простым соотношением
Еа = А * R, А = Еа / R (2.13)
Где R – универсальная газовая постоянная.
R = 
Подставив в уравнение (2.12) величину А из уравнения (2.13), получим
1nK= - 
+ В (2.14)
Дифференцируя (2.14) по температуре при Еа = const прейдем к уравнению:
(2.15)
которое называется уравнением Аррениуса в дифференциальном виде.
Из него путем интегрирования можно получить уравнение (2.14), где В постоянное интегрирование. Обозначив В = 1nK0 из уравнения (2.14) получим:
1nK = 1nK0 – Еа/RТ (2.16)
Или
К = К0 * е-Еа/RТ (2.17)
Глее К0 – предэкспоненциальный множитель константы скорости реакции (т.е. множитель стоящий перед показательной функцией).
Уравнение (2.17) называется уравнение Аррениуса в интегральной форме. Величины Еа и К0 определяются природой реакции и практически не зависят от температуры.
Энергию активации можно рассчитать по экспериментальным данным графическим или аналитическим способом.
Графический способ заключается в нахождении величины А = - tg α по графику зависимости 1nK = f (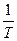) для данной реакции с последующим расчетом Еа по уравнению Еа = А * R.
Аналитический способ представляет применение уравнения (2.16) для двух различных температур (Т2 > Т1; К(т2) = К2; К(т1) = К1):
1nK2 = 1nK0 – Еа/RТ2
1nK1 = 1nK0 – Еа/RТ1
В результате вычитания второго уравнения из первого получим
1n 
(2.14)
По уравнению (2.14) можно рассчитать энергию активации данной реакции, используя два экспериментальных значения константы скорости при двух различных температурах, или произвести пересчет константы скорости с одной температуры на другую, если известна энергия активации.
