Под химическим равновесием понимают неизменное во времени состояния системы, содержащей как исходные вещества, так и продукты реакции, рассматриваемые обычно при постоянных давлении (Р), объеме (V) и температуре (Т).
Выделяют три основных признака истинного химического равновесия:
1. При отсутствии внешнего воздействия состав системы (так называемый равновесный состав) сохраняется постоянным сколь угодно долго.
2. К состоянию равновесия система может подойти со стороны как прямой (слева направо), так и обратной (справа налево) реакций.
3. Всякое, даже очень незначительное внешнее воздействие (изменение температуры, давления, концентраций реагирующих веществ) снижает равновесие в ту или иную сторону, система приходит к новому состояния равновесия.
Таким образом, вследствие химической обратимости реакции не доходят до конца. А так как, химически обратимые реакции до перехода в состояние равновесия протекают с конечными скоростями, с термодинамической точки зрения они необратимы и работа их не является максимальной.
Однако можно мысленно представить, что эти реакции в прямом и обратном направлениях идут бесконечно медленно через равновесные состояния, т.е. термодинамически обратимо. Тогда к ним можно применять общие условия термодинамического равновесия.
dG = 0 и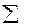 
μi 
= 0
Рассмотрим в условиях равновесия (р,Т = const) гомогенную газовую реакцию типа:
аА + bВ 
сС + dD
где а, b, с, d – стехиометрические коэффициенты веществ А, В, С, D. Обозначим через μА, μВ, μС, μD химические потенциалы этих веществ при равновесии. Применим соотношение 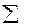μi = 0, выражающее условие равновесия, для нашей реакции, т.е.
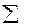μi = сμС + dμD - аμА - bμВ.
Для веществ А и В химический потенциал берется с минусом, потому что эти вещества расходуются и их химический потенциал убывает. Предположим, что ко всем участникам реакции применимы законы идеальных газов и в частности соотношение (1.80) μi = μi0 + RT lnpi . Подставляя значение μi в 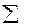μi и группируя соответствующие слагаемые получим:
сμС + dμD - аμА - bμВ + RT (сlnpС + dlnpD - аlnpА - blnpВ) = 0 или
ln 
(сμ0С + dμ0D - аμ0А - bμ0В) (1.83)
Все члены правой части этого равенства являются функциями только температуры, поэтому правая, а следовательно и левая части уравнения (1.83) при каждой данной температуре являются постоянными. Обозначим эту постоянную через ln Кp и перепишем уравнение (1.83) в виде
lnp 
= ln Кp откуда
Кр (1.84)
Постоянная Кр, в которую в данном случае входят равновесные парциальные давления компонентов, называется константой равновесия.
Уравнение (1.84) является термодинамическим выражением закона действующих масс: отношение произведения равновесных парциальных давлений продуктов реакции взятых в степенях, равных их стехиометрическим коэффициентам, к аналогичному произведению для исходных веществ есть величина постоянная при данной температуре.
Закон действующих масс впервые вывели Гульдберг и Вааге. (иногда этот закон называют их именем).
Для приведенной ранее обратимой реакции можно привести еще одну форму записи закона действующих масс:
Кс = 
(1.85)
В выражении (1.85) константа равновесия выражена через равновесные молярные концентрации исходных веществ и продуктов реакции.
Использую уравнения состояния Менделеева-Клапейрона для i – го компонента смеси идеальных газов рiv = v iRT легко установить взаимосвязь между константами химического равновесия.
Кс = Кр 
(1.86)
