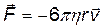,
где r – радиус шарика; v – его скорость.
Формула справедлива для скоростей, при которых число Рейнольдса много меньше единицы (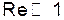
).
УПРУГИЕ ДЕФОРМАЦИИ ТВЕРДОГО ТЕЛА
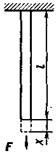• Относительная деформация при продольном растяжении или сжатии тела:
,
где 
— относительное удлинение (сжатие); x — абсолютное удлинение (рис. 4.1); l — начальная длина тела.
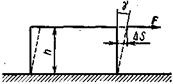
Относительная деформация при сдвиге определяется из формулы:
,
где 
— относительный сдвиг; Δ s — абсолютный сдвиг параллельных слоев тела относительно друг друга; h — расстояние между- слоями; 
— угол сдвига. (Для малых углов 
)
• Напряжение нормальное:
,
где 
— упругая сила, перпендикулярная поперечному сечению тела; S — площадь этого сечения.
Напряжение тангенциальное:
,
где — упругая сила, действующая вдоль слоя тела; S — площадь этого слоя.
• Закон Гука для продольного растяжения или сжатия:
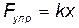или 
,
где k — коэффициент упругости (в случае пружины — жесткость); Е — модуль Юнга.
Закон Гука для сдвига:
,
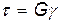где G — модуль поперечной упругости (модуль сдвига).
• Момент, закручивающий на угол φ однородный круглый стержень:
,
где 
— постоянная кручения.
• Потенциальная энергия растянутого или сжатого стержня при однородной деформации:
или 
;
при неоднородной деформации: 
где V — объем тела; объемная плотность энергии растянутого или сжатого стержня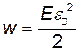 
ЗАКОНЫ ИДЕАЛЬНЫХ ГАЗОВ
· Количество вещества — число структурных элементов (молекул, атомов, ионов и т. п), содержащихся в системе или теле. Количество вещества выражается в молях. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в изотопе углерода 
массой 0,012 кг. Количество вещества:
= N / NA
где N — число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему); NA — постоянная Авогадро:
NA =6,02×1023 моль-1.
· Молярная масса вещества:
,
где m — масса однородного тела (системы); — количество вещества этого тела.
· Относительная молекулярная масса вещества:
,
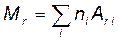где ni — число атомов i -го химического элемента, входящего в состав молекулы данного вещества; 
— относительная атомная масса этого элемента. Относительные атомные массы приводятся в таблице Д. И. Менделеева.
· Связь молярной массы М с относительной молекулярной массой Mr вещества:
,
где k =10-3 кг/моль.
· Молярная масса смеси газов
,
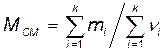где mi — масса i -го компонента смеси; vi — количество вещества i -го компонента смеси; k — число компонентов смеси.
· Массовая доля i -го компонента смеси газов
,
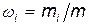где mi — масса i -го компонента смеси; m — масса смеси.
· Уравнение состояния идеальных газов (уравнение Клапейрона — Менделеева)
или 
,
где m — масса газа; М — его молярная масса; R — молярная газовая постоянная; Т — термодинамическая температура; — количество вещества.
· Закон Дальтона:
,
где p — давление смеси газов; pi — парциальное давление i -го компонента смеси; k — число компонентов смеси.
· Концентрация частиц (молекул, атомов и т. п.) однородной системы
,
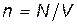где V — объем системы.
ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
· Связь между молярной (
) и удельной (с) теплоемкостями газа
,где М — молярная масса газа.
· Молярные теплоемкости при постоянном объеме и постоянном давлении соответственно равны (в целях упрощения записи в индексах обозначений молярной теплоемкости при постоянном давлении и постоянном объеме букву «
» будем опускать)
; 
,
где 
для газа одноатомных молекул, 
для газа двухатомных молекул, 
для газа трех- и более атомных молекул; 
— молярная газовая постоянная.
· Уравнение Майера
.
· Показатель адиабаты
.
· Внутренняя энергия идеального газа
,
где 
— количество вещества.
· Работа, связанная с изменением объема газа, в общем случае вычисляется по формуле
,
где V 1 — начальный объем газа; V 2 — его конечный объем.
Работа газа:
а) при изобарном процессе (p =const)
;
б) при изотермическом процессе (T =const)
;
в) при адиабатном процессе
, или 
,
где T 1 — начальная температура газа; T 2 — его конечная температура.
· Уравнение Пуассона (уравнение газового состояния при адиабатном процессе)
.
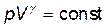· Связь между начальным и конечным значениями параметров состояний газа при адиабатном процессе:
.
· Первое начало термодинамики в общем случае записывается в виде
Q=DU+A,
где Q – количество теплоты, сообщённое газу; DU —изменение его внутренней энергии; А — работа, совершаемая газом против внешних сил.
Первое начало термодинамики:
а) при изобарном процессе
б) при изохорном процессе (A =0)
;
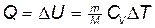в) при изотермическом процессе (D U =0)
,
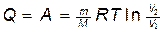г) при адиабатном процессе (Q =0)
.
· Термический коэффициент полезного действия (КПД) цикла в общем случае
,
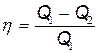где Q 1 – количество теплоты, полученное рабочим телом (газом) от нагревателя; Q 2 – количество теплоты, переданное рабочим телом охладителю.
КПД цикла Карно
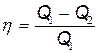, или 
,
где T 1 — температура нагревателя; T 2 — температура охладителя.
· Изменение энтропии
где A и B — пределы интегрирования, соответствующие начальному и конечному состояниям системы. Так как процесс равновесный, то интегрирование проводится по любому пути.
Примеры решения задач
Пример 1. Вода подается в фонтан из большого цилиндрического бака (рис. 19) и бьет из отверстия II—II со скоростью v2= 12 м/с. Диаметр D бака равен 2м, диаметр d сечения II—II равен 2 см. Найти: 1) скорость v1 понижения воды в баке; 2) давление p1, под которым вода подается в фонтан; 3) высоту h1 уровня воды в баке и высоту h2 струи, выходящей из фонтана.
Решение. 1. Проведем сечение I—I в баке на уровне сечения II—II фонтана. Так как площадь S1 сечения I—I много больше площади S2 (рис. 19) сечения II—II, то высоту h1 уровня воды вбакеможно считать длямалого промежутка времени постоянной, а поток – установившимся. Для установившегося потока справедливо условие неразрывности струи: v1S1 = v2S2 откуда v1 = v2S2 / S1, или
v1 = v2 (d/D) 2. (1)
Подставив значения заданных величин в (1) и произведя вычисления, найдем
v 1=0,0012 м/с.
С такой же скоростью будет понижаться уровень в баке. Как видно, эта скорость очень мала по сравнению со скоростью струи.
2. Давление p 1, под которым вода подается в фонтан, найдем по уравнению Бернулли. В случае горизонтальной трубки тока оно имеет вид
. (2)
Учтя, что p2 =0 (под давлением подразумевается избыточное над атмосферным давление), из уравнения (2) получим
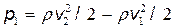. (3)
Так как v1 << v2, то из равенства (3) следует
.
После вычислений, произведенных по этой формуле, найдем
p 1 = 72 кПа.
3. Высоту h1 уровня воды в баке найдем из соотношения 
, откуда
.
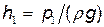Произведя вычисления по этой формуле, найдем
h 1=7,35 м.
Зная скорость v2, с которой вода выбрасывается фонтаном, найдем высоту h2, на которую она будет выброшена:
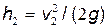=7,35 м.
Подчеркнем, что высота уровня воды в баке равна высоте, на которую поднимается фонтан воды (по правилу сообщающихся сосудов). Это замечание справедливо, если пренебречь сопротивлением воздуха.
Пример 2. В сосуде с глицерином падает свинцовый шарик. Определить максимальное значение диаметра шарика, при котором движение слоев глицерина, вызванное падением шарика, является еще ламинарным. Движение считать установившимся.
Решение. Если в вязкой жидкости движется тело, то вместе с ним, как одно целое, движется и прилипший к телу слой жидкости. Этот слой вследствие внутреннего трения увлекает за собой и соседние слои. Возникающее при этом движение жидкости является ламинарным или турбулентным в зависимости от размеров, формы тела и его скорости. Характер движения зависит также от свойств жидкости и определяется безразмерным числом Рейнольдса.
Если тело, движущееся в жидкости, имеет форму шара диаметром d, то число Рейнольдса определяется по формуле
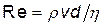, (1)
а критическое значение этого числа Re кр =0,5.
Скорость v выразим, исходя из следующих соображений. На свинцовый шарик, падающий в глицерине, действуют три силы:
1) сила тяжести шарика
,
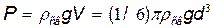где 
св — плотность свинца; V— объем шарика;
2) выталкивающая сила, определяемая по закону Архимеда
,
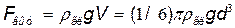где гл —плотность глицерина;
3) сила внутреннего трения, определяемая по формуле Стокса,
.
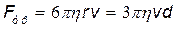При установившемся движении шарика в жидкости (v =const) сила тяжести шарика уравновешивается суммой выталкивающей силы и силы внутреннего трения, т. е.
,
откуда
(2)
Решая совместно уравнения (1) и (2) относительно d, найдем
.
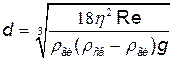Максимальное значение диаметра dmax при котором движение остается еще ламинарным, соответствует критическому значению числа Рейнольдса Re кp. Поэтому
.
Подставив сюда значения величин h = 1,48 Па·с; Re кp =0,5; cв =11300 кг/м3; гл =1260 кг/м3 и произведя вычисления, получим
dmax =5,29 мм.
Пример 3. Верхний конец стального стержня длиной l = 5 м с площадью поперечного сечения S = 4 см2 закреплен неподвижно, к нижнему подвешен груз массой 
кг. Определить: 1) нормальное напряжение 
материала стержня; 2) абсолютное х и относительное ε удлинения стержня; 3) потенциальную энергию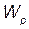 
растянутого стержня.
Решение. 1. Нормальное напряжение материала растянутого стержня выражается формулой 
, где F — сила, действующая вдоль оси стержня. В данном случае F равна силе тяжести mg и поэтому можем записать
.
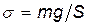Сделав вычисления, найдем
МПа.
2. Абсолютное удлинение выражается формулой
,
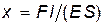где Е — модуль Юнга.
Подставив значения величин F, l, S и Е в эту формулу (значение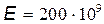 
Па из справочных данных) и произведя вычисления, получим
.
Относительное удлинение стержня
=2,46·10-4.
3. Потенциальная энергия растянутого стержня 
,
где V — объем тела, равный S × l.
Выполнив вычисления по этой формуле, получим
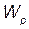= 12,1 Дж.
Пример 4. Найти молярную массу М смеси кислорода массой m 1=25 г и азота массой m 2=75 г.
Решение. Молярная масса смеси М см есть отношение массы смеси т см к количеству вещества смеси см т. е.
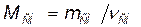. (1)
Масса смеси равна сумме масс компонентов смеси m см= m 1+ m 2. Количество вещества смеси равно сумме количеств вещества компонентов.
Подставив в формулу (1) выражения m см и см, получим
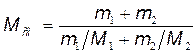. (2)
Молярные массы M 1 кислорода и М 2 азота:
M 1 =32×10-3 кг/моль, М 2=28×10-3 кг/моль. Подставим значения величин в (2) и произведем вычисления:
Пример 5. Определить: 1) число N молекул воды, занимающей при температуре t= 4°C объем V = 1 мм3; 2) массу m 1 молекулы воды; 3) диаметр d молекулы воды, считая, что молекулы имеют форму шариков, соприкасающихся друг с другом.
Решение. 1. Число N молекул, содержащихся в теле некоторой массы m, равно произведению постоянной Авогадро n a на количество вещества : 
. Так как 
, где М — молярная масса, то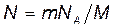 
. Выразив в этой формуле массу как произведение плотности r на объем V, получим
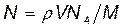. (1)
Все величины, кроме молярной массы воды, входящие в (1), известны: r =l×103 кг/м3, V =1 мм3=1×10-9 м3, n a=6,02×1023 моль-1.
Зная химическую формулу воды (Н2О), найдем молярную массу воды:
M= M r k= (2×1+1×16)×10-3 кг/моль=18×10-3 кг/моль. Подставим значения величин в (1) и произведем вычисления:
N= [1×103×1×10-9/(18×10-3)] 6,02×1023 молекул=3,34·1019 молекул.
2. Массу одной молекулы воды найдем делением ее молярной массы на постоянную Авогадро: m 1= M / n a. Произведя вычисления по этой формуле, получим
.
3. Будем считать, что молекулы плотно прилегают друг к другу, тогда на каждую молекулу диаметром d приходится объем (кубическая ячейка) V 1= d 3. Отсюда
. (2)
Объем V 1 найдем, разделив молярный объем V m вещества на число молекул в моле, т. е.на постоянную Авогадро n a: V 1= V m/ n a. Молярный объем равен отношению молярной массы к плотности вещества, т. е. V m= M / r. Поэтому можем записать, что V 1= M /(rn a).Подставив полученное выражение V 1 в формулу (2), получим
. (3)
Проверим, дает ли правая часть выражения (3) единицу длины:
.
Теперь подставим значения величин в формулу (3) и произведем вычисления:
d =3,11×10-10 м=311 пм.
Пример 6. В баллоне объемом V = 10 л находится гелий под давлением 
=1 МПа при температуре T 1=300 К. После того как из баллона был израсходован гелий массой m =10 г, температура в баллоне понизилась до T 2=290 К. Определить давление 
гелия, оставшегося в баллоне.
Решение. Для решения задачи воспользуемся уравнением Клапейрона – Менделеева, применив его дважды к начальному и конечному состояниям газа. Для начального состояния уравнение имеет вид
p 1 V =(m 1/ M) RT 1, (1)
а для конечного состояния –
p 2 V =(m 2/ M) RT 2, (2)
где m 1 и m 2 — массы гелия в начальном и конечном состояниях.
Выразим массы m 1 и m 2 гелия из уравнений (1) и (2):
m 1= Mp1V /(RT 1); (3)
m2=Mp2V/(RT2); (4)
Вычитая из (3) равенство (4), получим
.
Отсюда найдем искомое давление:
. (5)
Проверим, дает ли правая часть формулы (5) единицу давления. Для этого выразим все величины, входящие в нее, в соответствующих единицах. Единица, в которой выражается первое слагаемое, не вызывает сомнений, так как отношение T 2/ T 1 — величина безразмерная. Проверим, в каких единицах выражается второе слагаемое:
Убедившись в том, что правая часть полученной расчетной формулы дает единицу искомой величины – давления, можем подставить в (5) значения всех величин и произвести вычисления.
В формуле (5) все величины, кроме молярной массы М гелия, известны. Для гелия как одноатомного газа относительная молекулярная масса равна его относительной атомной массе А r.
Из таблицы Д. И. Менделеева найдем А r=4. Следовательно, молярная масса гелия М= А r×10-3 кг/моль =4×10-3 кг/моль. Подставив значения величин в (5), получим
.
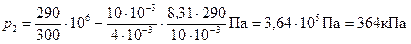Пример 7. Определить количество теплоты, поглощаемой водородом массой m =0,2 кг при нагревании его от температуры t 1=0°С до температуры t 2=100 °С при постоянном давлении. Найти также изменение внутренней энергии газа и совершаемую им работу.
Решение. Количество теплоты Q, поглощаемое газом при изобарном нагревании, определяется по формуле
Q=mcpDT, (1)
где m — масса нагреваемого газа; cp — его удельная теплоемкость при постоянном давлении; D T — изменение температуры газа.
Как известно, 
. Подставив это выражение c p в формулу (1), получим
,
где (молекула водорода двухатомная); 
кг/моль – молярная масса водорода.
