Электростатика и постоянный ток 1 страница

Основные формулы

ЗАКОН КУЛОНА. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

· Закон Кулона

,

где F — сила взаимодействия двухточечных зарядов Q₁ и Q₂; r — расстояние между зарядами; e — диэлектрическая проницаемость среды; e₀ — электрическая постоянная:

.

Закон сохранения заряда

,

где — алгебраическаясумма зарядов,входящихв изолированную систему; n — число зарядов.

· Напряженность электрического поля

,

где — сила, действующая на точечный положительный заряд Q, помещенный в данную точку поля.

· Сила, действующая на точечный заряд Q, помещенный в электрическое поле

.

· Поток вектора напряженности электрического поля:

а) через произвольную поверхность S, помещенную в неоднородное поле,

или ,

где a — угол между вектором напряженности и нормалью к элементу поверхности; — площадь элемента поверхности; E_n — проекция вектора напряженности на нормаль;

б) через плоскую поверхность, помещенную в однородное электрическое поле

Ф _E=ЕS cosa.

· Поток вектора напряженности через замкнутую поверхность

,

где интегрирование ведется по всей поверхности.

· Теорема Остроградского — Гаусса. Поток вектора напряженности через любую замкнутую поверхность, охватывающую заряды Q_l, Q₂,..., Q_n

,

где — алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; п — число зарядов.

· Напряженность электрического поля, создаваемого точечным зарядом Q на расстоянии r от заряда

.

Напряженность электрического поля, создаваемого металлической сферой радиусом R, несущей заряд Q, на расстоянии r от центра сферы:

а) внутри сферы (r<R) E =0;

б) на поверхности сферы (r = R) ;

в) вне сферы (r>R) .

· Принцип суперпозиции (наложения) электрических полей, согласно которому напряженность результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей:

.

В случае двух электрических полей с напряженностями и модуль вектора напряженности

,

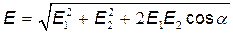где a — угол между векторами и .

· Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) нарасстоянии r от ее оси

,

где t — линейная плотность заряда.

Линейная плотность заряда распределенного по нити (цилиндру) есть величина, равная заряду, приходящемуся на единицу ее длины:

· Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,

где s — поверхностная плотность заряда.

Поверхностная плотность заряда распределенного по поверхности есть величина, равная заряду, приходящемуся на единицу этой поверхности:

.

· Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями, с одинаковой по модулю поверхностной плотностью заряда (поле плоского конденсатора)

.

Приведенная формула справедлива для вычисления напряженности поля между пластинами плоского конденсатора (в средней части его) только в том случае, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.

· Электрическое смещение связано с напряженностью электрического поля соотношением

.

Это соотношение справедливо только дляизотропных диэлектриков.

· Циркуляция вектора напряженности электрического поля есть величина, численно равная работе по перемещению единичного точечного положительного заряда вдоль замкнутого контура. Циркуляция выражается интегралом по замкнутому контуру , где E_l – проекция вектора напряженности в данной точке контура на направление касательной к контуру в той же точке.

В случае электростатического поля циркуляция вектора напряженности равна нулю:

.

 

ПОТЕНЦИАЛ. ЭНЕРГИЯ СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ. РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА В ПОЛЕ

· Потенциал электрического поля есть величина, равная отношению потенциальной энергии точечного положительного заряда, помещенную в данную точку поля, к этому заряду

j = 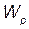/Q,

или потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к этому заряду:

j =A/Q.

Потенциал электрического поля в бесконечности условно принят равным нулю.

Отметим, что при перемещении заряда в электрическом поле работа A_в.с внешних сил равна по модулю работе A_с.п сил поля и противоположна ей по знаку:

A_в.с= – A_с.п.

· Потенциал электрического поля, создаваемый точечным зарядом Q на расстоянии r от заряда,

.

· Потенциал электрического поля, создаваемого металлической, несущей заряд Q сферой радиусом R, на расстоянии r от центра сферы:

внутри сферы (r < R) ;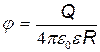

на поверхности сферы (r = R) ;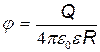

вне сферы (r>R) .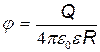

Во всех приведенных для потенциала заряженной сферы формулах e есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.

· Потенциал электрического поля, созданного системой п точечных зарядов, в данной точке в соответствии с принципом суперпозиции электрических полей равен алгебраическойсуммепотенциалов j₁, j₂,..., j_n, создаваемых отдельными точечными зарядами Q₁, Q₂,..., Q_n:

.

· Энергия W взаимодействия системы точечных зарядов Q₁, Q₂,..., Q_n определяется работой, которую эта система зарядов может совершить при удаленииих относительно друг друга в бесконечность, и выражается формулой

,

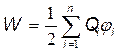где — потенциал поля, создаваемого всеми п– 1 зарядами (за исключением i -го) в точке, где расположен заряд Q_i.

· Потенциал связан с напряженностью электрического поля соотношением

.

В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой

,

или в скалярной форме

,

а в случае однородного поля, т. е. поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению

,

где j₁ и j₂ — потенциалы точек двух эквипотенциальных поверхностей; d – расстояние между этими поверхностями вдоль электрической силовой линии.

· Работа, совершаемая электрическим полем при перемещении точечного заряда Q из одной точки поля, имеющей потенциал j₁, в другую, имеющую потенциал j₂

A = Q (j₁ – j₂), или

где E_l — проекция вектора напряженности на направление перемещения; dl — перемещение.

В случае однородного поля последняя формула принимает вид

A=QElcosa,

где l — перемещение; a — угол между направлениями вектора и перемещения .

• Диполь есть система двух точечных электрических зарядов равных по размеру и противоположных по знаку, расстояние l ме­жду которыми значительно меньше расстояния r от центра диполя до точек наблюдения.

Вектор проведенный от отрицательного заряда диполя к его положительному заряду, называется плечом диполя.

Произведение заряда | Q | диполя на его плечо называется электрическим моментом диполя:

.

· Напряженность поля диполя

или ,

где р - электрический момент диполя; r - модуль радиуса-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует; α- угол между радиусом-вектором и плечом диполя.

· Потенциал поля диполя

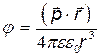или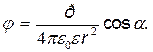

· Механический момент, действующий на диполь с электрическим моментом 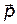, помещенный в однородное электрическое поле с напряженностью

или M=pE sin ,

где α- угол между направлениями векторов 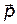и .

В неоднородном электрическом поле кроме механического момента (пары сил) на диполь действует еще некоторая сила. В случае поля, обладающего симметрией относительно оси х,сила выражается соотношением

где - частная производная напряженности поля, характеризующая степень неоднородности поля в направлении оси х.

При сила F _хположительна. Это значит, что под действием ее диполь втягивается в область сильного поля.

• Потенциальная энергия диполя в электрическом поле

 

ЭЛEКTPИЧECКAЯ EMКOCTЬ. КOHДEHCATOPЫ

· Электрическая емкость уединенного проводника или конденсатора

C =Δ Q /Δ φ,

где Δ Q - заряд, сообщенный проводнику (конденсатору); Δ φ - изменение потенциала, вызванное этим зарядом.

· Электрическая емкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью ε

Если сфера полая и заполнена диэлектриком, то электроемкость ее от этого не изменяется.

· Электрическая емкость плоского конденсатора

,

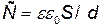где S - площадь пластин (каждой пластины); d - расстояние между ними; ε – диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Электрическая емкость плоского конденсатора, заполненного п слоями диэлектрика толщиной d_i каждый с диэлектрическими проницаемостями , (слоистый конденсатор)

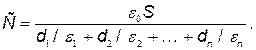
· Электрическая емкость сферического конденсатора (две концентрические сферы радиусами R ₁и R ₂, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε)

· Электрическая емкость цилиндрического конденсатора (два коаксиальных цилиндра длиной l и радиусами R ₁и R ₂, пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ε)

· Электрическая емкость С последовательно соединенных конденсаторов:

в общем случае 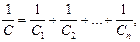где п - число конденсаторов;

в случае двух конденсаторов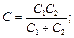

в случае п одинаковых конденсаторов с электроемкостью С₁ каждый

C=C ₁ /n.

· Электрическая емкость параллельно соединенных конденсаторов:

в общем случае C=C ₁ +C ₂ +...+C _n;

в случае двух конденсаторов C=C ₁ +C ₂;

в случае п одинаковых конденсаторов с электроемкостью С₁ каждый C=nC ₁.

 

ЭНЕРГИЯ ЗАРЯЖЕННОГО ПPOBOДHИКA. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

· Энергия заряженного проводника выражается через заряд Q, потенциал φ и электрическую емкость С проводника следующими соотношениями:

.

· Энергия заряженного конденсатора

где С - электрическая емкость конденсатора; U - разность потенциалов на его пластинах.

· Объемная плотность энергии (энергия электрического поля, приходящаяся на единицу объема)

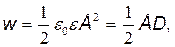
где Е - напряженность электрического поля в среде с диэлектрической проницаемостью ε; D - электрическое смещение.

 

ОСНОВНЫЕ ЗАКОНЫ ПОСТОЯННОГО ТОКА

· Сила постоянного тока

I=Q/t,

где Q - количество электричества, прошедшее сечение проводника за время t.

· Плотность электрического тока есть векторная величина, равная отношению силы тока к площади S поперечного сечения проводника:

где - единичный вектор, по направлению совпадающий с направлением движения положительных носителей заряда.

· Сопротивление однородного проводника

R=ρl/S,

где ρ - удельное сопротивление вещества проводника; l - его длина.

· Проводимость G проводника и удельная проводимость γ вещества

G= 1 /R, γ =l/ ρ.

· Зависимость удельного сопротивления от температуры

ρ=ρ ₀(1 +αt),

где ρ и ρ ₀ - удельные сопротивления соответственно при t и 0 ˚С; t -температура (по шкале Цельсия); α – температурный коэффициент сопротивления.

· Сопротивление соединения проводников:

последовательного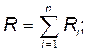

параллельного

Здесь R_i - сопротивление i- гопроводника; п - число проводников.

· Закон Ома:

для неоднородного участка цепи

для однородного участка цепи ;

для замкнутой цепи .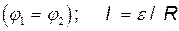

Здесь (φ ₁ – φ ₂) - разность потенциалов на концах участка цепи; ε ₁₂ - ЭДС источников тока, входящих в участок; U - напряжение на участке цепи; R - сопротивление цепи (участка цепи); ε - ЭДС всех источников тока цепи.

· Правила Кирхгофа.

Первое правило: алгебраическая сумма сил токов, сходящихся в узле, равна нулю, т. е.

где n - число токов, сходящихся в узле.

Второе правило: в замкнутом контуре алгебраическая сумма напряжений на всех участках контура равна алгебраической сумме электродвижущих сил, т.е.

где I _i - сила тока на i- мучастке; R _i - активное сопротивление на i- мучастке; ε_i- ЭДС источников тока на i- мучастке; п - число участков, содержащих активное сопротивление; k- число участков, содержащих источники тока.

· Работа, совершаемая электростатическим полем и сторонними силами в участке цепи постоянного тока за время t

A=IUt.

· Мощность тока

P=IU.

· Закон Джоуля - Ленца

Q=I ² Rt,

где Q - количество теплоты, выделяющееся в участке цепи при протекании постоянного тока за время t.

В случае переменного тока количество теплоты, выделяющееся за малое время

,

где – мгновенная сила тока.

Закон Джоуля - Ленца справедлив при условии, что участок цепи неподвижен и в нем не совершаются химические превращения.

Примеры решения задач

 

Пример 1. Три одинаковых положительных заряда Q₁ = Q₂ = Q₃ =1 нКл расположены по вершинам равностороннего треугольника (рис. 23). Какой отрицательный заряд Q₄ нужно поместить в центре треугольника, чтобы сила притяжения с его стороны уравновесила силы взаимного отталкивания зарядов, находящихся в вершинах?

Решение. Все три заряда, расположенных по вершинам треугольника, находятся в одинаковых условиях. Поэтому для решения задачи достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы один из трех зарядов, например Q₁,

находился в равновесии.

В соответствии с принципом суперпозиции на заряд действует каждый заряд независимо от остальных. Поэтому заряд Q₁ будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю:

, (1)

где — силы, с которыми соответственно действуют на заряд Q₁ заряды Q₂, Q₃ и Q₄; — равнодействующая сил .

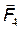Так как силы и направлены по одной прямой, то векторное равенство (1) можно заменить скалярной суммой:

F – F₄ =0, или F₄ = F.

Выразив в последнем равенстве F через F₂ и F₃ и учитывая, что F₃ = F₂, получим

.

Применяя закон Кулона и имея в виду, что Q₂ = Q₃ = Q₁, найдем

,

откуда

. (2)

Из геометрических построений в равностороннем треугольнике следует, что

.

С учетом этого формула (2) примет вид

.

Подставив сюда значение Q₁, получим

Q₄ =0,58 нКл.

Отметим, что равновесие системы зарядов будет неустойчивым.

 

Пример 2. Два заряда 9 Q и - Q закреплены на расстоянии l =50 см друг от друга. Третий заряд Q₁ может перемещаться только вдоль прямой, проходящей через заряды. Определить положение заряда Q₁, при котором он будет находиться в равновесии. При каком знаке заряда равновесие будет устойчивым? Равновесие называется устойчивым, если при малом смещении заряда от положения равновесия возникают силы, возвращающие его в положение равновесия.

Решение. Заряд Q₁ будет находиться в равновесии в том случае, если векторная сумма сил, действующих на него, будет равна нулю. Это значит, что на заряд Q₁ должны действовать две силы, равные по модулю и противоположные по направлению. Рассмотрим, на каком из трех участков I, II, III (рис. 24) может быть выполнено это условие. Для определенности будем считать, что заряд Q₁ —положительный.

На участке I (рис. 24, а) на заряд Q₁ действуют две противоположно направленные силы: и . Сила , действующая со стороны заряда 9 Q, в любой точке этого участка будет больше, чем сила , действующая со стороны заряда - Q, так как больший (по модулю) заряд 9 Q всегда находится ближе к заряду Q₁, чем меньший заряд - Q. Поэтому равновесие на этом участке невозможно.

На участке II (рис. 24, б) обе силы и направлены в одну сторону — к заряду - Q. Следовательно, и на втором участке равновесие невозможно.