,
где J 0 — момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси; а — расстояние между осями; m — масса тела.
• Момент импульса вращающегося тела относительно оси:
.
• Закон сохранения момента импульса:
,
где Li — момент импульса i -го тела, входящего в состав системы. Закон сохранения момента импульса для двух взаимодействующих тел:
где 
— моменты инерции и угловые скорости тел до взаимодействия: 
— те же величины после взаимодействия.
Закон сохранения момента импульса для одного тела, момент инерции которого меняется:
,
где 
— начальный и конечный моменты инерции; 
— начальная и конечная угловые скорости тела.
• Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси:
,
где 
— момент силы, действующей на тело в течение времени dt;
J — момент инерции тела; 
— угловая скорость; 
— момент импульса.
В случае постоянного момента инерции основное уравнение динамики вращательного движения принимает вид
,
где 
— угловое ускорение.
• Работа постоянного момента силы М, действующего на вращающееся тело:
A=Mj,
где j — угол поворота тела.
• Мгновенная мощность, развиваемая при вращении тела,
.
• Кинетическая энергия вращающегося тела
.
• Кинетическая энергия тела, катящегося по плоскости без скольжения:
,
где 
— кинетическая энергия поступательного движения тела; v — скорость центра инерции тела; 
,— кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр инерции.
РЕЛЯТИВИСТСКАЯ МЕХАНИКА
В специальной теории относительности рассматриваются только инерциальные системы отсчета. Во всех задачах считается, что оси у, у' и z, z' сонаправлены, а относительная скорость v 0 системы координат К' относительно системы К направлена вдоль общей оси хх'.
• Релятивистское (лоренцево) сокращение длины стержня:
где l 0 — длина стержня в системе координат К',относительно которой стержень покоится (собственная длина). Стержень параллелен оси х'; l — длина стержня, измеренная в системе К,относительно которой он движется со скоростью 
; с — скорость распространения электромагнитного излучения.
• Релятивистское замедление хода часов
,
где Δ t 0 — интервал времени между двумя событиями, происходящими в одной точке системы 
, измеренный по часам этой системы (собственное время движущихся часов); Δ t — интервал времени между двумя событиями, измеренный по часам системы K.
• Релятивистское сложение скоростей
,
где 
— относительная скорость (скорость тела относительно системы K '); 
— переносная скорость (скорость системы K ' относительно К), — абсолютная скорость (скорость тела относительно системы К).
В теории относительности абсолютной скоростью называется скорость тела в системе координат, условно принятой за неподвижную.
• Релятивистский импульс:
.
• Полная энергия релятивистской частицы
,
где T — кинетическая энергия частицы; 
— ее энергия покоя. Частица называется релятивистской, если скорость частицы сравнима со скоростью света, и классической, если 
.
• Связь полной энергии с импульсом релятивистской частицы:
.
• Связь кинетической энергии с импульсом релятивистской частицы
.
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
• Уравнение гармонических колебаний:
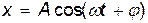
где х — смещение колеблющейся точки от положения равновесия;
t — время; А, ω, φ — соответственно амплитуда, угловая частота,
начальная фаза колебаний; 
— фаза колебаний в момент t.
• Угловая частота колебаний:
, или 
,
где ν и Т — частота и период колебаний.
• Скорость точки, совершающей гармонические колебания:
.
• Ускорение при гармоническом колебании
.
• Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле:
где А 1и А 2 — амплитуды составляющих колебаний; φ 1 и φ 2— их начальные фазы.
• Начальная фаза φ результирующего колебания может быть найдена из формулы:
.
• Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами ν 1 и ν 2,
.
• Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами A 1 и A 2 и начальными фазами φ 1 и φ 2:
.
• Дифференциальное уравнение гармонических колебаний материальной точки:
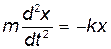, или 
,
где m — масса точки; k — коэффициент квазиупругой силы (
).
• Полная энергия материальной точки, совершающей гармонические колебания:
.
• Период колебаний тела, подвешенного на пружине (пружинный маятник):
,
где m — масса тела; k — жесткость пружины. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).
Период колебаний математического маятника
,
где l — длина маятника; g — ускорение свободного падения.
Период колебаний физического маятника
,
где J — момент инерции колеблющегося тела относительно оси колебаний; а — расстояние центра масс маятника от оси колебаний; 
— приведенная длина физического маятника.
Приведенные формулы являются точными для случая бесконечно малых амплитуд. При конечных амплитудах эти формулы дают лишь приближенные результаты. При амплитудах не более 
ошибка в значении периода не превышает 1 %.
Период крутильных колебаний тела, подвешенного на упругой нити:
,
где J — момент инерции тела относительно оси, совпадающей с упругой нитью; K — жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.
• Дифференциальное уравнение затухающих колебаний
или 
,
где r — коэффициент сопротивления; δ — коэффициент затухания: 
; ω 0— собственная угловая частота колебаний 
.
• Уравнение затухающих колебаний:
где A(t) — амплитуда затухающих колебаний в момент t; ω — их угловая частота.
• Угловая частота затухающих колебаний:
.
• Зависимость амплитуды затухающих колебаний от времени
,
где А 0 — амплитуда колебаний в момент t =0.
• Логарифмический декремент колебаний:
,
где A(t) и A(t+T) — амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.
• Дифференциальное уравнение вынужденных колебаний
или 
,
где 
— внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; F0 — ее амплитудное значение; 
.
• Амплитуда вынужденных колебаний:
.
• Резонансная частота и резонансная амплитуда:
и 
.
Примеры решения задач
Пример 1. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x=A+Bt+Ct 3, где A =4 м, B =2 м/с, С =-0,5 м/с3. Для момента времени t 1=2 с определить:
1) координату x 1 точки, 2) мгновенную скорость v 1, 3) мгновенное ускорение a1.
Решение. 1. Координату точки, для которой известно кинематическое уравнение движения, найдем, подставив в уравнение движения вместо t заданное значение времени t 1:
x=A+Bt+Ct3.
Подставим в это выражение значения A, В, С, t 1 и произведем вычисления:
x 1=(4+4 - 0,5· 23) м=4 м.
2. Мгновенную скорость в произвольный момент времени найдем, продифференцировав координату х по времени: 
Тогда в заданный момент времени t 1 мгновенная скорость v 1=B+3C t 12.
Подставим сюда значения В, С, t 1 и произведем вычисления: v 1 =- 4 м/с.
Знак минус указывает на то, что в момент времени t1=2 с точка движется в отрицательном направлении координатной оси.
3. Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты х по времени:
Мгновенное ускорение в заданный момент времени t 1 равно a 1 =6Ct 1. Подставим значения С, t 1и произведем вычисления:
a 1=(-6 ·0,5· 2) м/с= - 6 м/с.
Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.
Пример 2. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R= 50 м. Уравнение движения автомобиля S (t) = A+Bt+Ct2, где A=10 м, B=10 м/с, С= – 0,5 м/с2. Найти: 1) скорость v автомобиля, его тангенциальное 
, нормальное а n. и полное а ускорения в момент времени t =5 с; 2) длину пути l и модуль перемещения | 
| автомобиля за интервал времени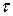 
=10 с, отсчитанный с момента начала движения.
Решение. 1. Зная уравнение движения, найдем скорость, взяв первую производную от координаты по времени:
.
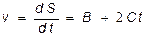Подставим в это выражение значения В, С, t и произведем вычисления:
v =5 м/с.
Тангенциальное ускорение найдем, взяв первую производную от скорости по времени: 
Подставив значение С, получим = ‑ 1 м/с2.
Нормальное ускорение определяется по формуле 
. Подставим сюда найденное значение скорости и заданное значение радиуса кривизны траектории и произведем вычисления:
an =0,5 м/с2.
Полное ускорение является геометрической суммой ускорений 
и 
: 
. Модуль ускорения 
. Подставив в это выражение найденные значения а 
и а n получим
а =1,12 м/с2.
2. Чтобы определить путь l, пройденный автомобилем, заметим, что в случае движения в одном направлении (как это имеет место в условиях данной задачи) длина пути l равна изменению криволинейной координаты 
т. е.
l = 
, или 
.
Подставим в полученное выражение значения В, С, 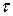и произведем вычисления:
l =50 м.
Модуль перемещения, как это видно из рис. 1, равен | 
|=2Rsin(
/2),
|
где 
— угол между радиусами-векторами, определяющими начальное 
и конечное 
положения автомашины на траектории. Этот угол (в радианах) находим как отношение длины пути l к радиусу кривизны R траектории, т. е. 
= l/R. Таким образом,
Подставим сюда значения R, l ипроизведем вычисления:
| |= 47,9м.
Пример 3. Маховик, вращавшийся с постоянной частотой 
0=10 с-1, при торможении начал вращаться равнозамедленно. Когда торможение прекратилось, вращение маховика снова стало равномерным, но уже с частотой = 6 с-1. Определить угловое ускорение 
маховика и продолжительность t торможения, если за время равнозамедленного движения маховик сделал N =50 оборотов.
Решение. Угловое ускорение маховика связано с начальной 
и конечной угловыми скоростями соотношением 
, откуда 
Но так как 
то
Подставив значения 
, , 0, N и вычислив, получим:
=3,14(62-102)/50 рад/с2= – 4,02 рад/с2.
Знак минус указывает на то, что маховик вращался замедленно. Определим продолжительность торможения, используя формулу, связывающую угол поворота 
со средней угловой скоростью 
вращения и временем t: 
. По условиям задачи, угловая скорость линейно зависит от времени и поэтому можно написать 
, тогда 
,
Откуда: 
Подставив числовые значения и произведя вычисления, получим
Пример 4. К концам однородного стержня приложены две противоположно направленные силы: F 1=40H и F 2=100 H (рис. 2, a).
|
Определить силу натяжения Т стержня в поперечном сечении, которое делит стержень на две части в отношении 1: 2.
Решение. Если бы силы F 1и F 2 были равны между собой, то сила натяжения в любом сечении стержня была бы одинаковой и равной силам, приложенным к концам стержня. Стержень в этом случае находился бы в покое. Но так как сумма сил, действующих на стержень, отлична от нуля, то стержень будет двигаться с ускорением, величина и направление которого определяются по второму закону Ньютона: 
, где т – масса стержня. Так как обе силы действуют вдоль прямой, то геометрическую сумму можно заменить алгебраической:
. (1)
При ускоренном движении стержня силы натяжения в разных сечениях различны. Для определения этих сил применим следующий прием: разделим стержень на две части в интересующем нас сечении и отбросим одну из них, например левую. Действие левой части на правую заменим силой натяжения Т (рис. 2, б ). В результате действия разности сил F2 – Т оставшаяся правая часть стержня массой m 1 должна двигаться с ускорением 
равным по величине и направлению прежнему ускорению, выражаемому формулой (1). Так как стержень однородный, то m 1 =m/ 3 и, следовательно,
. (2)
Приравнивая правые части равенства (1) и (2) и выражая из полученного равенства силу натяжения Т, находим
T=F 2 – (F 2 – F 1) / 3.
Подставив значения F 2 и F 1, получим
Т =80 Н.
Пример 5. В лифте на пружинных весах находится тело массой т= 10 кг (рис. 3, а). Лифт движется с ускорением а =2 м/с2. Определить показания весов в двух случаях, когда ускорение лифта направлено: 1) вертикально вверх, 2) вертикально вниз.
Решение. Определить показания весов — это значит найти вес тела G, т. е. силу, с которой тело действует на пружину. Но эта сила, по третьему закону Ньютона, равна по модулю и противоположна по направлению силе упругости N (силе реакции опоры), с которой пружина через посредство прикрепленной к ней чашки весов действует на тело, т. е.
или G=N. (1) Следовательно, задача определения показания весов сводится к нахождению реакции опоры N.
Задачу можно решать как в инерциальной, так и неинерциальной системе отсчета.
Решение в инерциальной системе отсчета. На тело действуют две силы: сила тяжести 
и сила 
.
Направим ось z вертикально вверх и спроецируем на нее все силы, действующие на тело. Индекс z у проекции сил опустим, так как проекции и сами силы совпадают по величине. Направление сил учтем знаком плюс или минус. Напишем уравнение движения:
, откуда 
. (2)
Из равенств (1) и (2) следует:
.
При вычислении показания весов следует учесть знак ускорения:
1) ускорение направлено вертикально вверх (a >0), тогда:
G 1=10(9,81+2)H=118 Н;
2) ускорение направлено вертикально вниз (a <0), тогда
G 2==10(9,81 – 2) Н=78 Н.
Отметим, что ни модуль, ни направление скорости лифта не влияют на показания весов. Существенны лишь величина и направление ускорения.
Решение в неинерциальной системе отсчета, т. е. в системе, движущейся ускоренно вместе с лифтом. В этой системе отсчета законы Ньютона не выполняются. Однако, если к телу в соответствии с принципом Даламбера дополнительно к действующим на него силам приложить силу инерции:
,
где а — ускорение системы отсчета, то с учетом этой силы законы Ньютона будут справедливы.
В этом случае на тело будут действовать три силы: сила тяжести , сила упругости и сила инерции 
; (рис. 3, б). Под действием этих сил тело в данной неинерциальной системе отсчета покоится. Это значит, что вместо уравнений динамики (законов Ньютона) можно воспользоваться законами статики. Если тело под действием системы сходящихся сил покоится, то геометрическая сумма этих сил равна нулю. В данном случае это приводит к равенству:
