Выборочное наблюдение – это несплошное наблюдение, при котором в случае правильной организации на отбор подлежащих обследованию единиц не может повлиять ничто, кроме случая. Сформированная таким образом совокупность изучается, а полученные результаты распространяются на всю исходную совокупность. Правильная организация выборочного наблюдения предполагает, что отобранная часть единиц в уменьшенном масштабе репрезентирует (представляет) всю совокупность в целом.
В торговле с помощью выборочного метода изучается качество поступивших товаров, эффективность новых форм торговли, спрос населения на определённые виды товаров, уровень цен на товары и др.
Совокупность, из которой производится отбор единиц, называется генеральной и все её обобщающие показатели генеральными.
Совокупность отобранных единиц именуется выборочной и все её показатели выборочными.
Основная задача выборочного наблюдения в экономике — получить достоверные суждения о показателях средней количественного признака и доли альтернативного признака в генеральной совокупности на основе характеристик выборочной совокупности.
Введём обозначения:
N – объём генеральной совокупности (число единиц в генеральной совокупности);
n – объём выборочной совокупности (число единиц в выборочной совокупности);
– генеральная средняя;
– выборочная средняя;
Р – генеральная доля (доля единиц, обладающих изучаемым признаком в генеральной совокупности: Р = 
, где М – число единиц, обладающих изучаемым признаком в генеральной совокупности);
W – выборочная доля (доля единиц, обладающих изучаемым признаком в выборочной совокупности: W =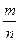 
, где m – число единиц, обладающих изучаемым признаком в выборочной совокупности).
1. По виду различают:
индивидуальный отбор – в выборочную совокупность отбирают отдельные единицы генеральной совокупности;
групповой отбор – в выборочную совокупность отбирают качественно однородные группы или серии изучаемых единиц;
комбинированный отбор – предполагает сочетание первого и второго вида.
2. По методу отбора различают:
повторный отбор – единица, попавшая в выборку, после регистрации признаков вновь возвращается в генеральную совокупность и таким образом приобретает возможность быть отобранной вновь;
бесповторный отбор – единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем отборе не участвует, т.е. численность единиц генеральной совокупности в процессе исследования сокращается.
3. По степени охвата единиц совокупности:
малые выборки – менее 30 единиц;
большие выборки.
4. По способу формирования выборочной совокупности:
собственно-случайный отбор;
механический отбор;
типический отбор;
серийный отбор;
комбинированный отбор;
многоступенчатый отбор.
Средняя ошибка выборки
Генеральные характеристики отличаются от выборочных на величину ошибки. Различают среднюю и предельную ошибку выборки. Величина средней ошибки рассчитывается дифференцированно в зависимости от способа отбора. Рассмотрим, как определяется средняя ошибка выборки при разных способах отбора.
1. Собственно-случайный отбор.
К собственно-случайной выборке относится отбор единиц из всей генеральной совокупности (без предварительного разбиения её на какие-либо группы) посредством случайного отбора, с использованием жеребьёвки, лотереи, таблицы случайных чисел.
Средняя ошибка при собственно-случайном способе отбора зависит от объёма выборки и степени варьирования изучаемого признака. Вариация изучаемого признака характеризуется величиной дисперсии. Формулы для расчёта средней ошибки приведены в таблице:
Средняя ошибка 
| Способ отбора единиц | |
| повторный | Бесповторный | |
| Для средней | 
| 
|
| Для доли | 
| 
|
где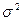 
– дисперсия выборочной средней;
w(1-w) – дисперсия выборочной доли.
2. Механический отбор.
Механическая выборка заключается в отборе единиц из генеральной совокупности через равные промежутки из определённого расположения их в генеральной совокупности (по алфавиту, в пространстве, последовательности появления во времени).
При достаточно большой совокупности механический отбор по точности результатов близок к собственно случайному отбору, поэтому для определения средней ошибки выборки используются те же формулы.
3. Типический отбор.
Типическая выборка используется в случае отбора единиц из неоднородной совокупности. Неоднородная исходная совокупность разбивается на несколько качественно однородных, однотипных групп по признакам, от которых зависят изучаемые показатели. Затем из каждой типической группы собственно-случайным или механическим способом отбора производится отбор индивидуальных единиц в выборочную совокупность. Общее число единиц выборочной совокупности распределяется между группами пропорционально численности групп в составе генеральной совокупности.
Типическая выборка даёт более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представительство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. Поэтому при определении средней ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.
Средняя ошибка типической выборки определяется по следующим формулам:
| Средняя ошибка
| Способы отбора единиц | |
| повторный | бесповторный | |
| Для средней: при пропорциональном размещении единиц |
|
|
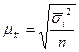
| Для доли: при пропорциональном размещении единиц |
|
|
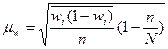
где 
– средняя из внутригрупповых дисперсий; выборочной среднего;
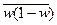– средняя из внутригрупповых дисперсий выборочной доли.
4. Серийный отбор.
Серийная выборка предполагает случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп (гнёзд, серий) с тем, чтобы в таких группах подвергать наблюдению все без исключения единицы (пачки, ящики и т.п.). Так как внутри групп (серий) обследуются все единицы, то средняя ошибка зависит только от межгрупповой (межсерийной) дисперсии.
Средняя ошибка выборки при серийном отборе определяется по следующим формулам:
| Средняя ошибка
| Способы отбора единиц | |
| повторный | бесповторный | |
| Для средней | 
| 
|
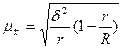
| Для доли |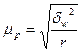 
| 
|
где R – число серий в генеральной совокупности;
r – число серий в выборочной совокупности;
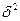– межгрупповая дисперсия выборочной средней;
– межгрупповая дисперсия выборочной доли.
Межгрупповая дисперсия выборочной доли определяется по формуле
где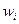 
– доля единиц, обладающих данным признаком в серии;
w – доля единиц, обладающих данным признаком во всей выборочной совокупности.
5. Комбинированный отбор.
В практике статистических обследований применяют также комбинации рассмотренных выше способов отбора — такой отбор называется комбинированным. Можно комбинировать серийную и случайную выборку, т.е. разбив генеральную совокупность на серии (группы) и отобрав нужное число серий, производят случайную выборку единиц из отобранных серий. Такая выборка может быть и повторной, и бесповторной, а средняя ошибка выборки при этом определяется:
при повторном отборе – 
при бесповторном отборе – 
где n – число единиц, взятое в выборку из серий.
6. Многоступенчатый отбор
Многоступенчатая выборка – из генеральной совокупности отбираются укрупнённые группы, далее ещё раз группы, меньшие по объёму, до тех пор, пока не будет отобрано обоснованное целью исследования количество групп или отдельных единиц, которые затем будут подвергнуты сплошному наблюдению. В отличие от типического отбора, целью которого является представительство в выборочной совокупности всех групп, при многоступенчатом отборе такая цель не ставится, а значит, не все группы попадают в выборку.
Если число ступеней отбора больше двух, то средняя ошибка выборки определяется по формуле
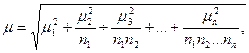
где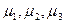 
… 
– средние ошибки выборки на отдельных ступенях отбора;
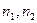… nn – численность выборок на соответствующих ступенях отбора.
Предельная ошибка выборки
Предельная ошибка выборки – максимально-возможная ошибка при достаточно большом числе независимых наблюдений. Согласно теореме П. Л. Чебышева (с уточнениями А.М. Ляпунова), при достаточно большом числе независимых наблюдений в генеральной совокупности с конечной средней и ограниченной дисперсией вероятность того, что расхождение между выборочной и генеральной средней (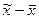
) не превысит по абсолютной величине некоторую величину 
, равна интегралу Лапласа (удвоенной нормированной функции Лапласа). Величина обозначаемая 
, называется предельной ошибкой выборки. Следовательно, предельная ошибка выборки:
для средней –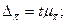 
для доли – 
где t – коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина придельной ошибки.
Значение коэффициента кратности (t) определяется в зависимости от принятой вероятности P по удвоенной нормированной функции Лапласа (приложение 1). Наиболее часто используемые значения следующие:
| T | 1,000 | 1,960 | 2,000 | 2,580 | 3,000 |
| Ф(t) | 0,683 | 0,950 | 0,954 | 0,990 | 0,997 |
