Вариация результативного признака обусловлена действием различных факторов, оценить влияние некоторых из них можно, разбив статистическую совокупность на группы по факторному признаку. Тогда вместе с изучением общей вариации признака в совокупности становится возможным изучить вариацию признака в каждой из составляющих её групп, а также между этими группами. В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации осуществляется с использованием трёх видов дисперсий.
1. Общая дисперсия  характеризует вариацию результативного признака в совокупности в результате действия всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака от общей средней и может быть вычислена по формулам:
характеризует вариацию результативного признака в совокупности в результате действия всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака от общей средней и может быть вычислена по формулам:
простая дисперсия для несгруппированных данных

взвешенная дисперсия для вариационного ряда

2. Межгрупповая дисперсия 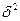 характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних
характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних  от общей средней
от общей средней  :
:

где f – численность единиц в группе.
3. Внутригрупповая дисперсия  отражает случайную вариацию, т.е. часть общей вариации, обусловленную влиянием неучтённых факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы xi (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная по соответствующим формулам:
отражает случайную вариацию, т.е. часть общей вариации, обусловленную влиянием неучтённых факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы xi (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная по соответствующим формулам:
простая дисперсия для несгруппированных данных  ;
;
взвешенная дисперсия для вариационного ряда –  .
.
На основании внутригрупповой дисперсии по каждой группе  , можно определить среднюю из внутригрупповых дисперсий
, можно определить среднюю из внутригрупповых дисперсий  :
:

Между всеми указанными дисперсиями существует взаимосвязь, которая называется правилом сложения дисперсий, — общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:

Другими словами, общая вариация признака в совокупности складывается из вариации признака внутри отдельных групп, вызванной действием всех неучтённых факторов, и вариации между группами, являющейся результатом действия только одного группировочного признака.
Для количественной оценки силы влияния признака, положенного в основание группировки, на образование общей вариации результативного признака в статистике используется эмпирический коэффициент детерминации:

Очевидно, что чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние признака, положенного в основание группировки, на изменчивость (вариацию) результативного (изучаемого) признака. При отсутствии связи между признаками эмпирический коэффициент детерминации равен нулю, при функциональной зависимости равен 1.
Эмпирическое корреляционное отношение – это корень квадратный из эмпирического коэффициента детерминации:
 .
.
Этот показатель используется для оценки тесноты связи между группировочным и результативным признаками. Принимает значение от 0 до 1. Если связь отсутствует, то эмпирическое корреляционное значение равно 0, т.е. все групповые средние равны между собой и межгрупповая вариация отсутствует. Значит, факторный признак, положенный в основание группировки, никак не влияет на образование общей вариации.
Если связь функциональная, то корреляционное отношение равно 1. В этом случае дисперсия групповых средних равна общей дисперсии, т.е. внутригрупповая дисперсия отсутствует. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака. Чем ближе значение корреляционного отношения к единице, тем теснее и ближе к функциональной связь между признаками.
Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока:
| Ŋ | 0,1–0,3 | 0,3 –0,5 | 0,5–0,7 | 0,7–0,9 | 0,9–0,99 |
| Сила связи | слабая | умеренная | заметная | тесная | весьма тесная |






