1. Размах вариации R (диапазон колебаний признака) — представляет собой разность между максимальным и минимальным значениями признака:
.
2. Среднее линейное отклонение 
– средняя арифметическая абсолютных значений отклонений отдельных вариантов от их средней арифметической без учёта знака:
Для несгруппированных данных:
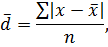
где n – число единиц совокупности;
Для вариационного ряда:
Где 
– сумма частот вариационного ряда.
3. Дисперсия признака 
представляет собой средний квадрат отклонений вариантов от их средней величины. В зависимости от исходных данных используют формулы:
– простая дисперсия для несгруппированных данных
– взвешенная дисперсия для вариационного ряда:
.
Рассчитать дисперсию можно также по преобразованной формуле
− квадрат среднего значения признака в совокупности;
− средний квадрат значений признака в совокупности:
При расчёте дисперсии по этой формуле исключается дополнительная процедура по учёту отклонений индивидуальных значений признака от его средней величины; за счёт этого уменьшается ошибка, связанная с округлением значений промежуточных вычислений.
4. Среднее квадратическое отклонение (
) – корень квадратный из дисперсии.
Это обобщающая 
характеристика размеров вариации признака в совокупности. Среднее квадратическое отклонение так же, как и среднее линейное отклонение показывает, насколько в среднем отклоняются конкретные варианты от их среднего значения.
Среднее квадратическое отклонение по своей величине всегда больше среднего линейного отклонения и является лучшей характеристикой меры колеблемости изучаемого признака.
Размах вариации, среднее линейное отклонение и среднее квадратическое отклонение являются именованными величинами, т.е. имеют ту же единицу измерения, что и изучаемый признак. Дисперсия единицы измерения не имеет.
Для оценки интенсивности вариации, а также для сравнения её величины в разных совокупностях или по разным признакам используют относительные показатели вариации, которые рассчитываются как отношение абсолютных показателей вариации к средней величине признака (или медиане) и выражаются в процентах:
коэффициент осцилляции 
;
относительное линейное отклонение 
;
коэффициент вариации 
По величине коэффициента вариации принято судить не только об интенсивности вариации признака, но и об однородности состава изучаемой совокупности. Чем больше значение коэффициента вариации, тем больше разброс значений признака вокруг средней, тем больше неоднородность совокупности. Общепринятым является следующее: совокупность считается однородной, если коэффициент вариации не превышает 33%.
