Под индексом в статистике понимают относительный показатель, характеризующий изменение величины какого-либо явления — простого или сложного, состоящего из соизмеримых или несоизмеримых элементов; во времени, пространстве или по сравнению с любым эталоном (нормативом, планом, прогнозом и т.д.).
По степени охвата единиц совокупности различают индивидуальные индексы и общие индексы. Индивидуальные индексы служат для оценки изменения индивидуального значения признака или для характеристики отдельных элементов сложного явления. Общие индексы характеризуют изменение величины какого-либо признака во всей совокупности в целом или отражают изменение всех элементов сложного явления. При этом под сложным явлением понимают такую совокупность, отдельные элементы которой непосредственно не подлежат суммированию (физический объём реализации продукции разного вида, цены на разные группы товаров и т.д.).
Индивидуальные индексы относятся к одному элементу (явлению) и не требуют суммирования данных:
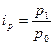 – индивидуальный индекс цен, где в числителе – цена единицы продукции в текущем (отчетном) периоде, а в знаменателе – цена единицы продукции в базисном периоде;
– индивидуальный индекс цен, где в числителе – цена единицы продукции в текущем (отчетном) периоде, а в знаменателе – цена единицы продукции в базисном периоде;
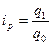 – индивидуальный индекс физического объёма продукции, в числителе – количество произведённой или реализованной продукции одного наименования в текущем (отчётном) периоде, а в знаменателе – количество произведённой или реализованной продукции в базисном периоде.
– индивидуальный индекс физического объёма продукции, в числителе – количество произведённой или реализованной продукции одного наименования в текущем (отчётном) периоде, а в знаменателе – количество произведённой или реализованной продукции в базисном периоде.
В экономических расчётах для измерения динамики сложного явления обычно используют общие индексы, которые могут быть построены двумя способами: как агрегатные и как средние из индивидуальных индексов.
Агрегатная форма индекса
Агрегатный индекс является основной формой индекса, числитель и знаменатель представляют собой «агрегат» (от лат. aggregatus — складываемый, суммируемый), составленный из напрямую не соизмеримых, а значит, не поддающихся суммированию элементов. Другими словами, в числителе и знаменателе агрегатного индекса содержится сумма произведений двух величин, одна из которых меняется (индексируется), а другая — остаётся неизменной и в числителе и в знаменателе (вес индекса) и служит для приведения к сопоставимому виду несоизмеримых величин. Умножение индексируемых величин на вес называется взвешиванием.
По содержанию индексируемых величин различают индексы количественных показателей и индексы качественных показателей.
Индексы количественных показателей – индексы физического объёма произведённой продукции, розничного товарооборота, национального дохода и др. В этих индексах индексируемые показатели являются объёмными и характеризуют общий, суммарный размер (объём) того или иного явления и выражаются абсолютными величинами. При расчёте таких индексов для соизмерения (сопоставления) используются качественные показатели, обычно зафиксированные на уровне базисного периода (цена, себестоимость, трудоёмкость).
Индексы качественных показателей – в этих индексах индексируемые показатели характеризуют уровень явления в расчёте на количественно измеримую единицу совокупности: цена за единицу продукции, себестоимость единицы продукции, трудоёмкость единицы продукции. Эти величины измеряют не общий объем явления, а интенсивность, эффективность явления или процесса. Обычно они являются либо средними, либо относительными величинами. Расчёт таких индексов производится на базе одинаковых неизменных значений количественного признака, зафиксированного, как правило, на уровне отчётного периода.
Агрегатный индекс физического объёма продукции является индексом количественного показателя:
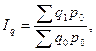
где 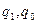 – количество (объём) продукции в натуральном выражении в отчётном и базисном периодах соответственно;
– количество (объём) продукции в натуральном выражении в отчётном и базисном периодах соответственно;
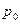 – базисная (фиксированная) цена;
– базисная (фиксированная) цена;
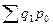 – условная стоимость произведённой или реализованной в текущем периоде продукции в ценах базисного периода;
– условная стоимость произведённой или реализованной в текущем периоде продукции в ценах базисного периода;
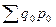 – фактическая стоимость произведённой или реализованной продукции в базисном периоде.
– фактическая стоимость произведённой или реализованной продукции в базисном периоде.
Разность числителя и знаменателя индекса физического объёма показывает, на сколько денежных единиц изменилась стоимость продукции (товарооборот) в результате роста (снижения) количества произведённой или реализованной продукции:
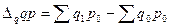
Агрегатный индекс цен является индексом качественного показателя:
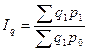 ,
,
где 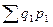 – фактическая стоимость товаров, произведённых или реализованных в отчётном периоде, в ценах отчётного периода;
– фактическая стоимость товаров, произведённых или реализованных в отчётном периоде, в ценах отчётного периода;
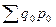 – условная стоимость товаров, произведённых или реализованных в отчётном периоде, в ценах базисного периода.
– условная стоимость товаров, произведённых или реализованных в отчётном периоде, в ценах базисного периода.
Разность между числителем и знаменателем индекса цен характеризует фактическую экономию (перерасход) покупателей, вызванную изменением цен:

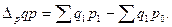
Индекс изменения стоимости произведённой или реализованной продукции – отношение общей стоимости произведённой или реализованной продукции в текущем периоде к общей стоимости произведённой или реализованной продукции в базисном периоде:
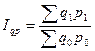 ,
,
где 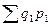 – фактическая стоимость продукции, произведённой или реализованной в текущем периоде, в ценах текущего периода;
– фактическая стоимость продукции, произведённой или реализованной в текущем периоде, в ценах текущего периода;
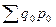 – фактическая стоимость продукции, произведённой или реализованной в базисном периоде, в ценах базисного периода.
– фактическая стоимость продукции, произведённой или реализованной в базисном периоде, в ценах базисного периода.
Этот индекс показывает, во сколько раз возросла (уменьшилась) стоимость произведённой продукции (товарооборота) в отчётном периоде по сравнению с базисным.
Разность между числителем и знаменателем индекса изменения стоимости произведённой продукции, показывает, на сколько денежных единиц изменилась стоимость продукции в текущем периоде по сравнению с базисным:
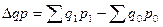
Индексный метод не только характеризует динамику сложного явления, но и позволяет оценить влияние, которое оказывают на результативный показатель отдельные факторы. Стоимость произведённой продукции равна произведению показателя стоимости основных фондов на фондоотдачу, товарооборот равен произведению количества реализованной продукции на соответствующую цену единицы продукции и т.д. Форма связи между такими показателями выявляется в ходе предварительного теоретического анализа, а затем измеряется количественно.
Связь между экономическими показателями находит отражение и во взаимосвязи характеризующих их изменения индексов, т.е. если 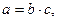 то
то 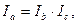 а если
а если 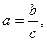 то и
то и 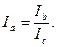
В качестве примера построения системы взаимосвязанных индексов рассмотрим индекс физического объёма, цен и стоимости продукции. Стоимость продукции является результативным показателем и зависит от физического объёма продукции и уровня цен на продукцию. Следовательно, произведение индекса физического объёма на индекс цен даёт индекс стоимости продукции (товарооборота в фактических ценах. Таким образом, индексы образуют индексную систему:
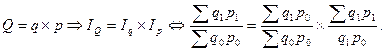
С помощью агрегатных индексов можно разложить общий абсолютный прирост результативного показателя на сумму приростов, вызванных действием отдельных факторов:
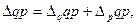
где 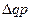 – абсолютный общий прирост стоимости продукции;
– абсолютный общий прирост стоимости продукции;
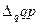 – абсолютный прирост стоимости продукции, вызванный изменением физического объёма произведённой или реализованной продукции;
– абсолютный прирост стоимости продукции, вызванный изменением физического объёма произведённой или реализованной продукции;
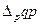 – абсолютный прирост стоимости продукции, вызванный изменением уровня цен произведённой или реализованной продукции.
– абсолютный прирост стоимости продукции, вызванный изменением уровня цен произведённой или реализованной продукции.
Средний взвешенный индекс
Агрегатный способ исчисления общих индексов в статистике является основным. Однако в торговле количественный учёт продажи товаров осуществляется лишь в оптовом звене. В розничной торговле реализация товаров учитывается в стоимостном выражении. Поэтому агрегатная форма общих индексов здесь не применяется. Основной формой общих индексов количественных и качественных показателей торговли является средняя взвешенная форма.
Если неизвестно количество реализованных отдельных видов продукции в натуральных измерителях в текущем периоде, но известны индивидуальные индексы физического объёма и стоимость отдельных видов продукции в базисном периоде, то можно рассчитать средний взвешенный арифметический индекс физического объёма продукции.
Исходной базой построения средневзвешенного индекса физического объёма продукции служит его агрегатная форма:
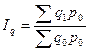 .
.
Знаменатель этой формулы известен, для нахождения числителя используют формулу индивидуального индекса физического объёма продукции:
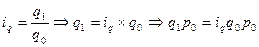 .
.
Подставим это выражение в числитель агрегатной формы индекса и получим общий индекс физического объёма в форме средневзвешенного арифметического индекса, где весами служит стоимость отдельных видов продукции в базисном периоде:
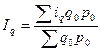 .
.
Индекс физического объёма может быть построен и по формуле средней гармонической взвешенной при наличии данных об индивидуальных индексах физического объёма и стоимости отдельных видов продукции в отчётном периоде:
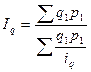 .
.
Если неизвестны цены на отдельные виды продукции, но известны индивидуальные индексы цен и стоимость отдельных видов продукции в отчётном периоде, то можно рассчитать средний взвешенный гармонический индекс цен.
Средневзвешенный индекс цен строится на основе его агрегатной формы:
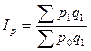 .
.
Числитель этой формулы известен. Для нахождения знаменателя используют формулу индивидуального индекса цен:
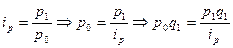 .
.
Подставим это выражение в знаменатель агрегатной формы индекса и получим общий индекс цен в форме средневзвешенного гармонического индекса, где весами служит стоимость отдельных видов продукции в отчётном периоде:
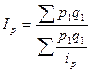 .
.
Если известны индивидуальные индексы цен и стоимость отдельных видов продукции в базисном периоде, то общий индекс цен может быть построен и по формуле средней арифметической взвешенной:
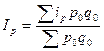 .
.
Такие же принципы положены в основу преобразования агрегатных форм других количественных и качественных показателей.






