Пределы для генеральных характеристик (доверительные интервалы) определяются на основе показателей, полученных по данным выборки. Доверительный интервал для генеральной средней:
 ;
;
 .
.
Доверительный интервал для генеральной доли:
 ;
;
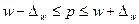 .
.
Определение необходимого объёма выборки
При проектировании выборочного наблюдения с заранее заданным значением допустимой ошибки выборки очень важно правильно определить численность (объём) выборочной совокупности, который с определённой вероятностью обеспечит заданную точность результатов наблюдения.
Формулы для определения необходимой численности выборки n легко получить непосредственно из формул предельной ошибки выборки. Так, при собственно-случайном способе отбора необходимая численность выборки составит:
| Численность выборки (n) | Способ отбора единиц | |
| повторный | Бесповторный | |
| Для средней | 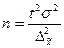
| 
|
| Для доли | 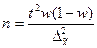
| 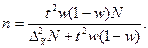
|
Эти формулы показывают, что с увеличением предполагаемой ошибки выборки значительно уменьшается её необходимый объём.
Решение типовых задач
Пример 4.1.
В городе было проведено выборочное обследование 1% граждан (случайный, повторный отбор) с целью изучения их доходов в ноябре.
| Месячный доход, руб. | 1200 – 4200 | 4200 – 7200 | 7200 – 10 200 | 10 200 и более |
| Число обследованных |
Определим:
1) среднемесячный доход у жителя города в ноябре, гарантируя результат с вероятностью 0,997;
2) долю жителей города с доходом 7 200 руб. и выше, гарантируя результат с вероятностью 0,954;
3) необходимую численность выборки при определении среднемесячного дохода, чтобы с вероятностью 0,997 предельная ошибка выборки не превышала 300 руб.;
4) необходимую численность выборки при определении доли жителей с доходом более 7 200 руб. и выше, чтобы с вероятностью 0,954 предельная ошибка не превышала 5%;
5) предельную относительную ошибку для выборочной средней и выборочной доли.
Решение
I. Среднее значение признака в выборке:

Дисперсия выборочной средней:

Предельная ошибка при вероятности 0,997 (коэффициент доверия 3):

Доверительный интервал:
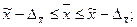

Таким образом, с вероятностью 0,997 можно утверждать, что средний доход жителей города в ноябре будет находиться в пределах от 6 509 до 6 991 руб.
2. Доля жителей города с доходом выше 7 200 руб. по данным выборочного наблюдения:
 .
.
Предельная ошибка при вероятности 0,954 (коэффициент доверия 2):
 .
.
Доверительный интервал:
 ;
;
 ;
;
 .
.
Таким образом, с вероятностью 0,954 можно утверждать, что в генеральной совокупности число жителей, имеющих доход свыше 7 200 руб., находится в пределах от 38,2 до 43,8%.
3. Для определения необходимой численности выборки при определении среднемесячного дохода с вероятностью 0,997 (коэффициент доверия) и предельной ошибкой не более 300 руб. воспользуемся формулой для расчёта предельной ошибки для средней при повторном отборе:

Таким образом, чтобы с вероятностью 0,997 ошибка выборки не превышала 300 руб., численность выборки должна составлять 775 человек.
4. Для определения необходимой численности выборки при определении доли жителей города с доходом более 7 200 руб. с вероятностью 0,954 (коэффициент доверия 2) и предельной ошибкой, не превышающего 5 %, воспользуемся формулой для расчёта предельной ошибки для доли при повторном отборе:
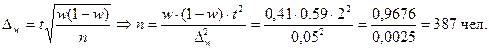
Таким образом, чтобы с вероятностью 0,954 ошибка выборки не превышала 5%, численность выборки должна составлять 387 человек.
5. Предельная относительная ошибка выборки определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:
для средней: 
для доли: 






