Вопрос о выборе средней решается в каждом отдельном случае, исходя из задачи исследования, материального содержания изучаемого явления и наличия исходной информации. Основное условие – величины, представляющие собой числитель и знаменатель средней, должны быть логически связаны между собой.
1. Средняя арифметическая – применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных её единиц.
Если данные не сгруппированы, т.е. не учитывается частота появления отдельного варианта в совокупности, то средняя арифметическая в этом случае будет называться простой:
где x1, х2, …xn – индивидуальные значения признака (варианты);
n – число единиц совокупности.
Средняя, рассчитанная из вариантов, которые повторяются различное число раз или имеют различный вес в совокупности, называется взвешенной. В качестве веса выступает численность единиц в разных группах, объединяющих одинаковые варианты. Таким образом, средняя арифметическая взвешенная используется в том случае, когда данные упорядочены и известны частоты отдельных вариантов:
где f1, f2,… fn – веса (частота повторения одинаковых признаков);
– сумма произведений величины признаков на их частоты;
– общая численность единиц совокупности.
В отдельных случаях веса могут быть представлены не абсолютными, а относительными величинами (в % или долях единицы): 
– частость, т.е удельный вес частоты отдельного варианта в общей сумме частот. Если частоты подсчитывают в долях (коэффициентах), то 
, и формула средней арифметической взвешенной имеет вид: 
. Если значения осредняемого признака заданы в виде интервалов вариационного ряда распределения, то при расчёте средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд.
2. Средняя гармоническая используется в тех случаях, когда статистическая информация не содержит частот fi отдельных вариантов xi в совокупности, а представлена их произведением xi∙fi = wi 
fi =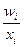 
:
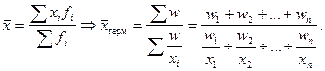
3. Средняя хронологическая – применяется в тех случаях, когда размер изучаемого явления задан на определённые даты (на определённые моменты времени):
,
где 
– значения признака на равностоящие друг от друга даты;
n – число дат.
Структурные средние
Структурные средние используются для изучения внутреннего строения множества или структуры распределения.
1. Мода – значение признака, наиболее часто встречающееся в изучаемой совокупности. В дискретном ряду модой является вариант, имеющий наибольшую частоту (частость). В интервальном вариационном ряду мода рассчитывается по формуле
где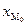 
– нижняя граница модального интервала;
– величина модального интервала;
– частоты (частости) соответственно модального, домодального и послемодального интервала.
Модальный интервал – это интервал, имеющий наибольшую частоту (частость) и содержащий точечное значение моды.
2. Медиана – вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части таким образом, что половина единиц совокупности имеют значение признака меньше, чем медиана, а половина – больше.
В интервальном вариационном ряду медиана определяется по формуле
где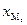 
– нижняя граница медианного интервала;
– величина медианного интервала;
– сумма частот (частостей) вариационного ряда;
– частота (частость) медианного интервала;
– сумма накопленных частот (частостей) в интервале, предшествующем медианному.
Медианный интервал – это интервал, в котором находится порядковый номер медианы. Для его определения необходимо подсчитать сумму накопленных частот (частостей) до числа, чуть превышающего половину объёма совокупности.
Решение типовых задач
Пример 2.1. Известны следующие данные о деятельности торгового предприятия:
| № магазина | Апрель | Май | |||
| численность продавцов | средний объём продаж одного продавца, тыс. руб. | среднемесячный объём продаж одного продавца, тыс. руб. | товарооборот, тыс. руб. | ||
Определим, за какой месяц и на сколько процентов был больше средний объём продаж одного продавца торгового предприятия.
Решение
Данные за апрель месяц упорядочены, известны частоты отдельных вариантов. Для расчёта среднего значения объёма продаж одного продавца в целом по торговому предприятию используем среднюю арифметическую взвешенную:
где f1, f2, fn – веса (частота повторения одинаковых признаков);
– сумма произведений величины признаков на их частоты;
– общая численность единиц совокупности.
= 92,19 тыс. руб.
В данных за май частоты не известны, а даётся показатель товарооборота, который находится как произведение численности продавцов (частота) на средний объем продаж одного продавца (осредняемый признак). В этом случае для расчёта среднего объёма продаж одного продавца в целом по торговому предприятию используется средняя гармоническая взвешенная:
,
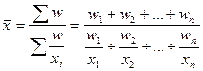= 95,85 тыс. руб.
Для оценки изменения во времени используем относительную величину динамики: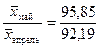 
= 1,0397, или 103,97%, т.е. прирост среднего объёма продаж одного продавца в целом по торговому предприятию в мае по сравнению с апрелем составил 3,97%.
Пример 2.2. Известны следующие данные о стоимости имущества торгового предприятия, млн руб.:
| Дата | млн руб. | дата | млн руб. |
| 01.01 | 01.08 | ||
| 01.02 | 01.09 | ||
| 01.03 | 01.10 | ||
| 01.04 | 01.11 | ||
| 01.05 | 01.12 | ||
| 01.06 | 01.01 | ||
| 01.07 |
Рассчитаем сумму налога на имущество, подлежащую уплате в бюджет, если ставка составляет 2,0 %.
Решение
Сумма налога на имущество, подлежащая уплате в бюджет, находится как произведение налоговой базы (стоимости имущества предприятия, признаваемого объектом налогообложения) на ставку налога. Стоимость имущества предприятия представлена по данным баланса на конкретные даты, а это значит, что их напрямую, как в случае с интервальными значениями, суммировать нельзя. Для расчёта среднего значения при таких исходных данных используется средняя хронологическая:
.
= 18,1 млн руб.
Тогда сумма, подлежащая уплате в бюджет, составит:
18,1 ∙ 0,02 = 0,362 млн руб.
Пример 2.3. Магазины торговой сети распределяются следующим образом по размеру товарооборота:
| Размер товарооборота, тыс. руб. | Число магазинов |
| До 50 | |
| 50–100 | |
| 100–150 | |
| 150–200 | |
| 200–250 | |
| 250–300 | |
| 300–350 | |
| 350–400 |
Определим средний размер товарооборота, моду и медиану.
Решение
1. Среднее значение признака для интервального ряда распределения:
,
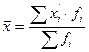где 
– середина соответствующего интервала.
тыс. руб.
2. Мода – наиболее часто встречающееся значение признака в совокупности. В интервальном ряду сначала определяется модальный интервал, т.е. интервал, который имеет наибольшую частоту: 200–250.
где 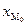– нижняя граница модального интервала;
– величина интервала;
– частота модального интервала;
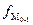– частота интервала, предшествующего модальному;
– частота интервала, следующего за модальным.
тыс. руб.
3. Медиана – это вариант, стоящий в середине ранжированного ряда. В интервальном ряду распределения сначала указывают медианный интервал, в котором сумма накопленных частот чуть превышает сумму частот ряда. Расчёт суммы накопленных частот приведён в таблице:
| Размер товарооборота, тыс. руб. | Число магазинов | Частости 
| Накопленные частости 
|
| До 50 | |||
| 50 – 100 | |||
| 100 – 150 | |||
| 150 – 200 | |||
| 200 – 250 | |||
| 250 – 300 | |||
| 300 – 350 | |||
| 350 – 400 | |||
| Свыше 400 | |||
| Итого |
Медианный интервал: (200 – 250)
,
где 
– нижняя граница медианного интервала;
– величина медианного интервала;
– сумма частот (частостей) вариационного ряда;
– накопленная частота интервала, предшествующего медианному;
– частота медианного интервала;
га.
