Если поверхность задана ур-ем F(х,у,z)=0 и точка Мо лежит на этой поверхности,то касательная плоскость к поверхности в точке Мо определяется ур-ем:
(Х-Хо) 
(Mo)+(У-Уo) 
(Mo)+(Z-Zo)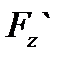 
(Mo)=0
Нормаль к поверхности в точке Мо-прямая,проходящая через точку Мо 
к касательной плоскости.
Точка поверхности F(x,у,z)=0, в которой одновременно обращаются в 0 все частные производные 1го порядка F '(x), F '(y)...называются особыми точками.В таких точках не имеет ни касательную к плоскости,ни Нормале.
Вопрос 55
Экстремум ф-ции нескольких переменных
Значение ф-ции u=f(x,y…t)=f(m) в т.Mo назыв максимализм (минимализм),если оно является наиб(наим)по сравнению с ее значением во всех достаточно близких m
Вопрос 56
Необходимые достаточные условия экстремум ф-ций нескольких переменных
Условия:
Ф-ция нескольких перемен может иметь max(min) экстремум только в т. Лежащих внутри области опред-я в которых ее частные производн 1-го порядка =0 или не сущ-ют необход уравн-е.Такие точки назыв критические.
В частности для ф-ции 2-х переменных f(x;y) критическ т.Mo в которой ф-ция дважды дифф-на и следует по знаку опред: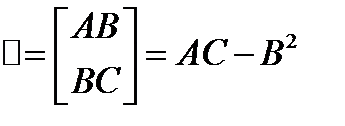 
A=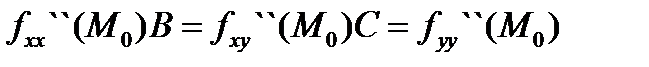 
1)если 
,то Mo-т. Экстремума
При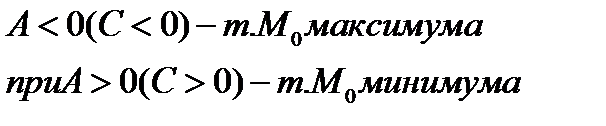 
2) 
то в т. Mo-экстрем нет
3)если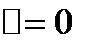 
,то для решения о наличии или отсутствие экстремума в т.Mo требуется дальнейшее иследоваие
Вопрос 57.
Наибольшее и наименьшее значение функции нескольких переменных в замкнутой области.Правило нахождения этих значений для функции двух переменных.
Определение этих значений такое же,как и для функции одной переменной.
Наиб. и наим. значение ф-ций нескольких переменных нельзя путать с её max и min,кот.являются наиб. и наим. по сравнению с её значениями в соседних точках.
Если ф-ция разрывна или непрерывна в незамкнутой области,то она может и не иметь наиб. и наим. значений.
Ф-ция u=f(x,y..t)=f(M),непрерывна в некоторой в неограниченной замкнутой области D.обязат.имеет в этой области наиб. и наим. значение.
Эти значения достигаются ею или в точках лежащих внутри области D или в точках,лежащих на границах области D.
Правило нахождения наиб. и наим. значений ф-ции f(M) в ограниченной замкнутой области D.
1.Найти критические точки лежащие внутри области D и вычислить значение ф.этих точек не исследуя будет ли экстремум и какого вида
2.Найти наиб.и наим. значение ф-ции на границах области.
3.Сравнить полученные значения,самое большее будет наиб.значением,а самое меньшее-наим.значением f(M) в области D
Вопрос 58.
Скалярное поле.Поверхности и линии уровня.
Скалярное поле-плоская или пространственная область с каждой точкой M,которой связано определенное значение некоторой скалярной величины U.
u=u(M) задание поля скалярной величины равносильно заданию скалярной (числовой) ф-ции.
Ф-ция u(М) определяющие плоское скалярное поле,зависит от 2х переменных u=u(x;y), а ф-ция u(M),определяющее пространственное сколярное поле зависит от 3х переменных u=u(x;y;z)
Линией уровня пл.скалярного поля наз-ся совокупность точек пл.,в котор.ф-ция этого поля имеет одинаковые значения.
Эт линия опред.следующим ур-м: u(x;y)=c, где С-Сonst.
Через каждую точку в этом случае проходит только 1 линия уровня. они заполняют всю рассматрив.область и не пересекаются между собой.
Поверхность уровня-это совокупность точек пространства в которых ф-ция этого поля имеет одинаковые значения,имеет вид: u(x;y;z)=с
Вопрос 59
.Производная по направлению.
Производная ф-ции и (М) по направлени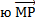 
= 
– предел отношения разности u(M₁)-u(M) направл.отрезка ММ₁,когда точка М₁ 
М оставаясь на прямой МР.
Производная ф-ции u(M) по направл. обозначается: 
Ф-ла::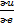 
= 
вычисляется по ф-ле: 
Если обозначим 
-норм.вектор.поверхности уровня,то: = 
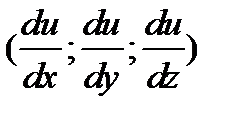
Обозначим -ед.векторов,вектора 
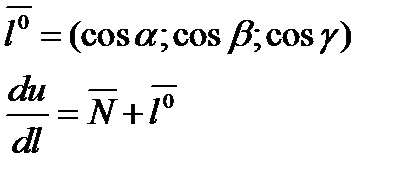
Вопрос 60.
Градиент скалярного поля и его свойства.
Градиент ф-ции(поля)-вектор определяемой ф-ции.
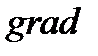u= 
……………направления grad u совпадает с направл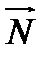 
поверхности или линии уровня.
Из всех произв-х ф-ции u (М) взятых по направлениям,наиб.значение имеет произв-ая по напр.градиента ф-ции.
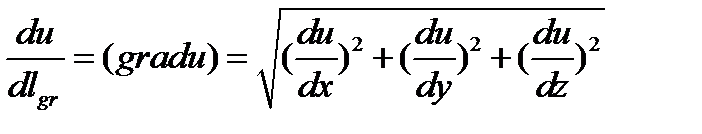
Градиент есть вектор наибыстрейшего возрастания ф-ции.
…….-скорость изменения ф-ции при перемещении (.)М по направлению вектора
