1)∫ sin^n x dx ∫cos^n x dx
А)∫ от четных степеней sin или cos находят понижением стпени:

Б)∫ от не четных степеней sin и cos находят отделяя от одного множителя один множитель и заменяя кофункцию новой переменной.
2)  Эти интегралы находятся по правилу а) где m и n - четные числа и по правилу б)
Эти интегралы находятся по правилу а) где m и n - четные числа и по правилу б)
Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)

3) Интегралы вида ∫tg^m xdx и ∫ctg^m xdx находят заменой td или ctg новой переменной, используя формулы:tg^2 x=(1/cos^2 x)−1,ctg^2 x=(1/sin^2 x)−1.
4)∫(sin ax*cos bx)dx ∫(sin ax*sin ax*sin bx)dx ∫(cos ax*cos bx)dx находят путем разложения на слогаемые:
Sin ax+cos bx=1/2(sin(a+b)x+sin(a-b)x)
Sin ax+sin bx=1/2(cos(a-b)x-cos(a+b)x)
Cos ax+cos bx=1/2(cos(a-b)x+cos(a+b)x
41. Площадь кривол.трапеции.Опред.интеграл,его св-ва
Пусть ф-ия у=f(x) непрерывна на отрезке  . 1) Разделим отрезок
. 1) Разделим отрезок  .на n частичных отрезков с длинами
.на n частичных отрезков с длинами  ,
,  2) Выбираем в каждом по 1произ-ой точке.
2) Выбираем в каждом по 1произ-ой точке. 

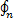 . 3) Вычислим значение ф-ии в этих точках f(
. 3) Вычислим значение ф-ии в этих точках f( ),f(
),f( ),…,f(
),…,f( ). 4) Составим сумму f(
). 4) Составим сумму f( )
)  + f(
+ f( )
)  + …+f(
+ …+f(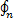 )
)  . =
. =  – интегральная сумма ф-ции f(x) на отрезке
– интегральная сумма ф-ции f(x) на отрезке  .
.
По разному деля отрезок  на n частичных отрезков и по разному выбирая в них по одной точке, можно составить бесчисленное множество различных интегральных сумм для f(x)
на n частичных отрезков и по разному выбирая в них по одной точке, можно составить бесчисленное множество различных интегральных сумм для f(x)  .
.
Но при неограниченном увеличении «n», т.е. 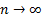 и стремится к 0 наибольшей из длин частичного отрезка все эти суммы имеют 1 общий предел, т.е. все они стремятся к одному и тому же.
и стремится к 0 наибольшей из длин частичного отрезка все эти суммы имеют 1 общий предел, т.е. все они стремятся к одному и тому же.
Общий предел всех этих интегральных сумм f(x) на  - определенный интегралом от ф-ции f(x) пределов от a до b, и обозначается
- определенный интегралом от ф-ции f(x) пределов от a до b, и обозначается 
Свойства: 1) При перестановке пределов изменяется знак интеграла. 
2) Интеграл с одинаковым 

3) Интеграл от алгеб. суммы ф-ции = алгеб.сумма слагаемых

4) Отрезок интегрирования можно разбивать на части:

5) Постоянную можно вынести за знак опред.интеграла:
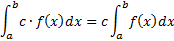
1. Криволинейная трапеция прилежит к оси Ох.
Если вся она расположенна над Ох,то ее [ 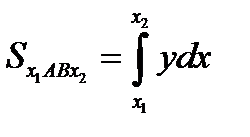 ]
]
Если криволинейная трапеция расположена ниже Ох,то f(x) 
и перед интегралом будет «-».
2. Криволинейная трапеция прилежит к оси Оу.
Если она расположена справа от оси Оу,то 
Если слева,то  (y)
(y)  .
.
42. Интеграл с переменным верхним пределом, формала ньютона-Лейбница.
Пусть на отрезке [ a, b ] задана непрерывная функция f (x), тогда для любого x  [ a, b ] существует функция:
[ a, b ] существует функция:

задаваемая интегралом с переменным верхним пределом, стоящим в правой части равенства.
На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла.
Из определения интеграла с переменным верхним пределом - функции F (x) и известных свойств интеграла следует, что при x  [ a, b ]
[ a, b ]
F' (x) = f (x).
Для вычисления опред.интеграла служит ф-ла Ньютона-Лейбница:

Опред.интеграл равен разности значений первообразной  на концах отрезка
на концах отрезка 
Вопрос 43
Вычисление определенных интегралов:замена переменной,интегрирование по частям.






