Пусть функция y = f(x) определена и непрерывна на отрезке [a; b]. Множество [a; b] является областью значений некоторой функции x = g(z), которая определена на интервале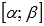 
и имеет на нем непрерывную производную, причем 
и 
, тогда 
.
Этой формулой удобно пользоваться в тех случаях, когда нам требуется вычислить интеграл 
Интегрирование по частям при вычислении определенного интеграла.
Пусть на отрезке [a; b] определены и непрерывны функции u(x) и v(x) вместе со своими производными первого порядка и функция 
– интегрируема, тогда на этом отрезке интегрируема функция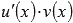 
и справедливо равенство 
.
Этой формулой удобно пользоваться в тех случаях, когда нам требуется вычислить интеграл
Вопрос 44)
применение определенного интервала.
1)вычисление S плоских фигур:
S всякой плоской фигуры отнесенной к прямоугольной системе координат может быть составима из S криволинейных тропеций относительных к оси Ох (прилегающих к оси Ох) или к оси Оу.
3. Криволинейная трапеция прилежит к оси Ох.
Если вся она расположенна над Ох,то ее [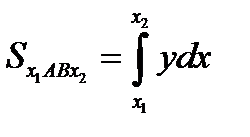 
]
Если криволинейная трапеция расположена ниже Ох,то f(x) 
и перед интегралом будет «-».
4. Криволинейная трапеция прилежит к оси Оу.
Если она расположена справа от оси Оу,то 
Если слева,то 
(y) .
3.S всякой плоской фигуры отнесенной к полярной системе координат может быть составлена из площадей кривол. AOB.
R=f(
2)вычисление объемов тел вращения:
Если тело образуется при вращении вокруг Ох
Криволин трапеции 
прилежащей к оси Ох,то
Объем тела вращения вычисляются по формуле:
[V=П 
dx(x1 
x2)]
К оси Оу:
Если тело образуется при вращении вокруг Оу кривол.
Трапецией 
, прилежащей к оси Оу,то объем
Тела вращения вычисляется: [V=П 
dy(y1 y2)]
3)длина дуги плоской кривой.
Если плоск.кривая относительно к прямоуг.системе коорд.
И задана уравнение 1)y=f(x) или 2) x=F(y) или k= 
(t)
Y=(t),то диферинциал длины дуги de выражается:
1)de= 
dx 2)dx=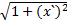 
dy 3)dy= 
dt
Длина дуги АВ определяются формулой:
Lab=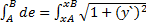 
dx= 
dy= 
Если плоская кривая отнесена к полярной системе координат и задана уравнением
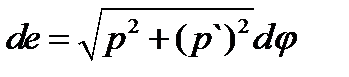
Вопрос 45)
несобственные интегралы –интегралы с бесконечными пределами интегрирования или от разрывных функций называются несобственными.
1. Несобственные интегралы с бесконечными пределами интегрирования. Опр. Посредством предельного перехода.
2.Несобственные интегралы от функции с бесконечными разрывами. Определяются посредством предельного перехода.
Если функция f(x) имеет бесконечный разрыв в точке C 
[ a;b] и непрерывна во всех других точках этого отрезка, то 
Несобственные интегралы называются сходящимися или расходящимися в зависимости от того, существуют или нет определяющие их соотв. Опред.интегралов.
Вопрос 46.
