Пусть зависимость ф-ии у и аргументов х, задана параметрически, т.е. в виде 2-х уравнений.
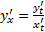
Логарифмическое дифференцирование.
Диф-е многих ф-ий упрощается если сначала логарифмируют, а полученный диф-ют, такую операцию наз-ют логариф-им дифф-ем. Логариф-ое диф-е применяют когда ф-ия содержит лог-ие операции (умнож.,деление, в степень, извлеч.корня). Или для нахождения производной от показательной степенной ф-ии.
Вопрос 22.
Уравнение касательной и нормали к плоской кривой.
Если точка М0(х0;у0) это точка касания, то угл. коэфф. косателной = произв-ой этой точки К=f ’(x0). Воспользуемся ур-ем прямой проходящ. через данную точку М0 в данном направлении. у-у0=К(х-х0), напишем ур-ие касательной у-у0=f’(x0)(x-x0) проходящ. через М0. Прямая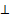 
касательной в точке касания наз. Нормалью кривой, т.к. она ⊥ к касательной, то Кнорм= 
= 
. Поэтому ур-е нормали к кривой в точке М0 -> у-у0= 
(x-x0), где f ’(x)≠0.
Вопрос 23.
Производные высших порядков,
Производная ф. у’=f(x), также является ф-ей от х, она наз. производной 1 порядка. Если ф-я у’=f’(x) дифферен., то ее производная наз. произ-ой 2 порядка и обозначается у’’ или f’’(x) или 
. y’’=(y’’)’ … общая ф-ла n-порядка - 
. Произ-ая порядка начиная со 2 и выше наз. произ-ми высших порядков.
Физический смысл II произ-ой: II произ-ая от пути по времени есть величина ускорения прямолин. движения точки.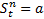 
– в этой формуле смысл II производной. Если ф-ия задана неявно (это когда «у»- не выражен) F(x;y)=0, то продифференцировав это ур-е по х и выразив из наилучшего результата у’ находим I-ую производную у’. Продеф-ав по х I производную находят II произ-ю. В нее будут входить у'; y; x. В этот результат нужно подставить вместо у’ найденное значение. Аналогично находится у’’’. Если ф-ия задана параметрически 
, то произ-ая находится по «х». 
находим 2 произ-ую 
, 
= 
, 
.
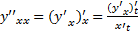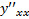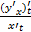формула Лейбница.
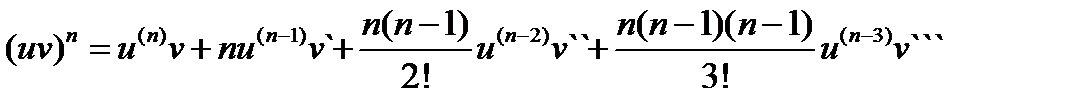
Вопрос 24.
Дифференциал функции, Пусть фун-ия у=f(x) имеет производную в точке х. f’(x)=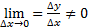 
. Воспользуемся теоремой: если 
, то сама 
будет = А+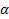 
, где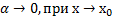 
, тогда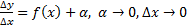 
Каждая из 2-х слагаемых является б.м.в. Сравним каждую из них с 
.
1-ое слагаемое и это б.м. одного порядка
– 2 слагаемоеб.м. более высокого порядка, чем , поэтому 1 слагаемое 
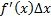называется главной частью приращения ф-ции 
.
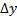Дифференциалом ф-ции 
, называется главная часть приращения ф-ции 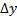обозначается
.
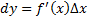Выразим , для этого рассмотрим 
и найдем ее дифференциал 
. 
.
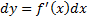дифференциал ф-ции = произведению производной этой ф-ции на дифференциал независимой переменной: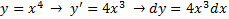 
Его геометрический смысл.
Проведем к графику ф-ции в точке 
касательную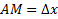 
, а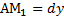 
. Найдем 
.
Рассматриваем 
: 
.
Дифференциал ф-ции в точке 
= приращению ординаты касательной проведенной к графику
ф-ции в этой точке – в этом геометрический смысл дифференциала.
Вопрос 25.
