Определение и обознаение:
Переменная u назыв ф-ей n переменных(аргументов x,y…t),если каждой системе значений x.y…t из области их изменений соотв опред значение u
U=f(x,y..t)
Геометрически:1)каждая с/с значений 2-х переменных(x;y) изображается точкой на пл-ти,а ф-ция 2-х переменных изображается некоторой поверхность в пространстве.
2)Каждая с/с значений 3-х переменных (x,y…t) отражается в т. Пространстве.
3)с/с значений 4-х и больше числа переменного не имеет геометр изображения,но в целях общности с/с значений любого числа n переменных (x,y….t) назыв т. N-мерного пространства,а ф-цию u зависящую от n переменных назыв ф-цией n-мерного пространства u=f(x,y…t)=f(M)
Областью опред ф-ции назыв совок всех точек в которых она имеет опред действ значение z=f(x;y)-для ф-ций 2-х переменных u=f(x,y..t)для ф-ций 3-х переменных совок некоторых точек пространства.
Вопрос 47.
Предел и не прерывность функции нескольких переменных.
Число A называется пределом функции f(m) в точке m0 lim f(M)=A. Если абсолютное знаечение разности |f(M)-f(M0)| будет меньше любого заранее заданного числа E>0 когда расстояние MM0 меньше некоторого числа 
>0 зависящего от эпсиона 
= 
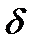(E).
Функция f(M) называется не прерывной в точке от M0 если lim f(M)=f(M0)
Для не прерывности функции f(M) в точке M0 необходимо выполнение трех условий.
1) F(M) должна быть определена в точке M0 и ее окрестности
2) F(M) должна иметь предел когда М 
М0 любым способом
3) Это предел должен быть равен F(M0)
Функция f(M) непрерывна в каждой точке области D- называется непрерывной в этой области.
Вопрос 48.
Частные производные первого порядка ф-ции нескольких переменных.
Ф-цию u=f(x,у...t) можно дифференцировать по каждому из её аргументов,считая все остальные аргументы постоянными.
Производная от ф-ции u`=f(x,у...t) по х взятая в предположении,что все остальные аргументы у...t постоянные,называются частной производной от фции u по х и обозначаются: 
или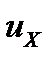 
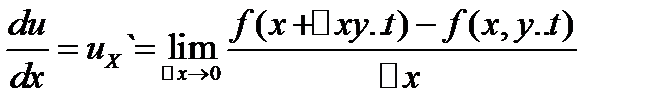
Аналогично определяются и обозначаются частные производные от u по остальным аргументам
Вопрос 49
Дифференц ф-ций и нескольких переменных.Применение полного дифференц приблженого вычисления.
Частным дифферен по x ф-ции u назыв главная часть соотв частного приращения ф-ции
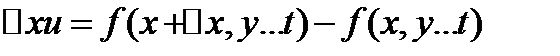аналогично опред частные дифф-лы ф-ции u по каждому из остальных ее аргументов.Они обозначаются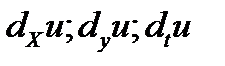 
Из их опред следует,что 
Полным диф-лом ф-ции u=f(x,y…t) назыв главная часть ее полного приращения 
Полный диф-л ф-ции если он сущ= 
∑ частных диф-лов
u=f(x,y…t)
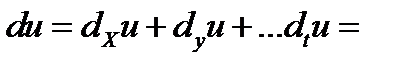
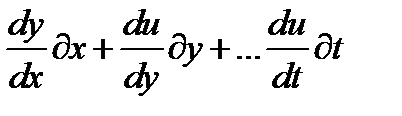
Ф-ция u=f(x,y…t) назыв диф-ой в т.(x,y…t) если она имеет в этой т полный диф-л
