Вопрос 1.
Числовое множество
Множество -совокупность некоторых объектов,объедененных по какому-либо признаку. Элементы -объекты,из которых состоит множ-во.Обозн-ют загл.лат.буквами (А,В...Х,Y). Пустое множ-во -множ-во,не содержащее не одного элемента. Элементы множ-ва записывают в фигурных скобках,в которых они или перечислены или указано их общее св-во. Прим: A={1;2;3;4}-т.е.множ-во А состоит из эл-тов 1,2,3,4. А={x:0 x 1}. Множ-во А называется подмножеством множества В,если каждый эл-т множ-ва А является эл-том множ-ва В. А с В-А вкючено в В
В с А-В включает в себя А
Множ-во А и В равны или совпадают (А=В),если А с В и В с А,т.е они состоят из одних и тех же эл-тов.
Объединение или сумма множеств А и В -множ-во,состоящее из эл-тов,каждое из которых принадлежит хотя бы 1-му из множ-в.
А.. В(А+В); A.. B={x: x.. A или х.. В}
Пересечение(произведение)множ -в А и В-множ-ва,состоящие из эл-тов,каждый из которых принадлежит множ-ву А и В.
А.. В={x: x.. A b x.. B}
Числовое множ -во-множ-во,элементы которого-числа. Пример:
N={1:2...n...}-множ-во натур-ых чисел; Zo={0;1;2;...n...}-множ-во целых неотриц.чисел; Z={0;+1;+2;...+n...}-множ-во целых чисел;
Q={m/n: m...Z; n...N}-множ-во рациональных чисел; R-множ-во действ.чисел.Между этими множ-ми существует соответствие:
N...Zo...Z...Q...R
Рациональные числа- выражаются коннечной или бесконечной периодической десятичной дробью.(0,25 или 0,333).
Иррациональные числа -действительное число,не являющееся рациональным(П=3,1415926....).Ирр.числа выражаются бесконечной непериодической десят. дробью.
Комплексные числа.
Введение множ-ва компл.чисел связано с тем,что во множ-ве действ.чисел не выполняется извлечение корня чётной степени из отриц. числа. Комплексное число(z)- упорядоченная пара действительных чисел. Алгебраическая форма компл.числа:
z=x+iy
x-действительная часть; у-мнимая часть компл. числа.
i-множит ед.
При х=0: z=0+iy-чисто мнимое
у=0: z=x+i0=x-действ.число
2 компл.числа равны,если Z1=Z2
всякое комплексное число z=x+iy можно изобразить точкой М(х;y) в плоскости ОХУ
y Комплексное число можно изобразить радиус-вектором 
M 
.
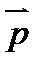
x
о
Величина угла между положит.направл ОХ и вектором 
называется аргументом z(Arg z)
Arg z=arg z+2пк(к=0: 
)
Arg z-величина многогранника
arg z –гл.значение аргумента,когда z=0+i0,то
Z=P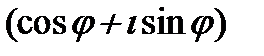 
-тригометрическая форма комплексного числа
1) 
2) 
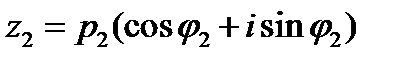
-ф-ла муавра
Для ее возведения комплексного числа в натур степень
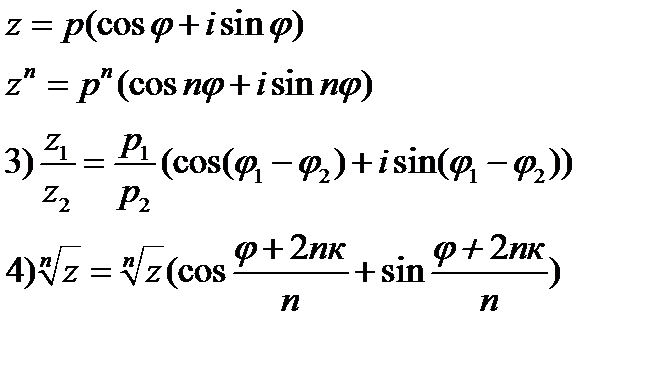
Вопрос 2.
Числовые промежутки.Окрестности точки.
Пусть а и в-действительные числа,причем а<в. Числовой промежуток(интервал)-подмножество всех действ. чисел,имеющие следующий вид:
[a; b]={x: a 
x 
b}-отрезок
(a;b]={x: a<x 
b}- пролуоткрый интервал
[a; b)={x: a 
x<b}- пролуткрытый интервал
(a; b)={x: a<x<b}- интервал
(- 
;b]={x: - 
<x b}-бесконечный интервал
(- ;b)={x: - <x<b}- бесконечный интервал
(a;b)={x: a<x<b}- бесконечный интервал
(a;b]={x: a<x b}- бесконечный интервал
(- ; 
)={x: - <x< 
}- бесконечный интервал
a и в называют левыми и правыми краями интервала.Пусть Xo-действительное число(точка на числовой прямой). Окрестностью точки Хо называют любой интервал,содержащий эту точку.В частности интервал (Xо- 
; Xo+ 
) (
>o) называют
эпсилон-окрестностью точки Хо.
Число Хо-центр
-радиус
Пусть точка Хо X 
(Xо- ; Xo+ ),то выполняется нер-во Xо- <X< Xo+ => |X-Xo|< 
- 
<X-Xo< 
Выполнение последнего нер-ва означает поподание точки Х в эпсилон-окрестность точки Хо.
Вопрос 3.
Функция
Пусть даны 2 непустых нож-ва х и у,соответствие f,которое каждому эл-ту х...Х составляет только 1 элеиент у,называется
ф-цией и записывается у=f (x)
Чётная функция - это такая функция, что f(-x)=f(x) для любой точки из области определения. График чётной функции симметричен относительно оси Оу.
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимой переменной.Нечётная фу́нкция симметрична относительно центра координат.
Возраст. Ф-ция: Функция y=f(x) возрастает на интервале X, если для любых и выполняется неравенство. Другими словами – большему значению аргумента соответствует большее значение функции.
Убыв. Ф-ция: Функция y=f(x) убывает на интервале X, если для любых и выполняется неравенство. Другими словами – большему значению аргумента соответствует меньшее значение функции.
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, т.е не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа на всей области определения.
Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции обычно обозначается
Вопрос 6.
Предел ф-ции в точке
Пусть ф-ция определена в некоторой окресности точки Хо кроме самой точки. Число а называется пределом ф-ции в точке Хо или при Х стремящемся к Хо (Х Хо),если для любого положительного эпсилона найдется положителное число,то для всех Х Хо и удовлетворяющих нер-ву |X-Xо|<0 выполняется нер-во | f(X)-A|<E
lim f(X)=A
Геометрический смысл предела ф-ции
Если для любой эпсилон-окрестности
точки А найдется такая окресность в
точке Хо,что для всех Х=Хо из этой
окресности соотв-щее зеачение
ф-ции f(X) лежит в эпсилон-окресности
точки А.
Величина зависит от выбора эпсилон.Поэтому:
Вопрос 7.
Односторонние пределы
В определении предела ф-ции Lim f(X)=A считается,что X стремится к Хо любым способом:
1)Оставаясь меньше Хо (слева от Хо)
2)Больше,чем Хо (справа от Хо)
3)Колеблясь вокруг точки Хо
Но бывают случаи,когда способ приближения Х к Хо влияет на значение предела ф-ции.По этому вводят односторонние пределы
Предел ф-ции слева обозначается lim f(x)=A
Предел ф-ции справа обозначается lim f(x)=A
Если существует предел,то существует оба односторонних предела,причем А1 =А2 =А. Верно и обратное утверждение: если существуют оба односторонних предела и они равны (А1 =А2),то сущ. И предел ф-ции,причём А1 =А2= А.
Если А1 = А2,то предел limf (X)- не существует.
Вопрос 8.
