Если в некотором интервале кривая расположена ниже любой своей касательной,то она называется выпуклой вверх на этом интервале
Если кривая расположена выше любой своей касательной,то она называется в ыпуклой вниз на этом интервале.
Точка прегиба -точка на кривой,где меняется направление ее выпуклости. Направление выпуклости кривой у=f (X) определяется знаком у '':
1.у ''>0- то ф-ция выпукла вниз.
2.у ''<0- то ф-ция выпукла вверх.
Правило нахождения абсцисс точек перегиба:
1. Найти у '' и точки,где у ''=0 или не сущ-ет,а кривая непрерывна и эти точки должны лежать внутри ООФ.
2.Определить знак у '' слева и справа от каждой из этих точек.Если по разные стороны Хо у '' имеет разные знаки,то Хо-точка перегиба.
Вопрос 33.
Асимптоты ГФ.
Асимптота кривой -такая кривая k,где неограниченно приближается точка кривой при удалении её от начала координат.
Для нахождения асимптот используют правило:
1.Если при х=а кривая у=f (x) имеет бесконечный разрыв (т.е.пр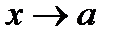и 
и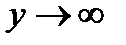 
), то кривая х=а явл. вертик.асимптотой
2.Неверт.асимптота кривой у= f (x):если они имеют ур-ие у=kx+b,где параметры а и b определяются ф-ми: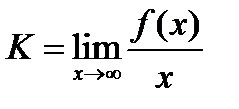 
Вопрос 34.
Общая схема исследования ф-ции и построение их граффика.
1.Найти ООФ
2.Найти точку разрыва и ее односторонний предел в этих точках
3.Выяснить на чётность/нечётность,непериодичность и т.д
4.Найти точки пересечения ГФ с осями координат и интервалы ф-ции,т.е. промежутки,в кот-ых f(x)>0 или f(x)<0
5.Найти асимптоты ГФ(не вертикальные)
6.Найти т.экстремума,интервали возраст. и убыв. Ф-ции
7.Найти т.перегиба ГФ и интервалы выпуклости его вверх или вниз
8.Построить ГФ не получая результат.
Вопрос 35.
Наибольшее и наименьшее значение ф-ции на отрезке
Ф-ция может иметь только одно наибольшее и наименьшее значение или может не иметь их совсем. Нахождение этих значений непрерывной ф-ции основано на след.св-вах:
1.Если в некотором интервале(конечном или бесконечном) ф-ция f(x) непрерывна и имеет только один экстремум и это max(min),то он будет наиб или наим. значением ф-ции в этом интервале.
2.Если f(x) непрерывна на некотором отрезке [a;b],то она обязательно имеет на этом отрезке наиб.,наим. значение.
Эти значения достигаются ею или в т.экстремума,лежащих внутри,или на его границах.Их этого следует правило нахождения наиб. и наим. значений f(x) на отр. [a;b],где она непрерывна:
1.Найти критич.точки внутри [a;b] и вычислить значение ф-ции в этих точках не выясняя будет ли она в них экстремумом и какого вида.
2.Вычислить значение f(x) на границах отрезка,т.е f(a) и f(b)
3.Сравнить полученный значения.(самое большое с наиб.,а самое меньшее с наим. значением ф-ции на отр. [a;b])
Вопрос 36.
Первообразная. Неопределенный интеграл и его свойства. Таблица интегралов.
Осн ф-лы интегрирования. Отыскание ф-ции F(x) по известному ее диф-лу и по известной произ-ой F`(x)=f(x),т.е.действие обратное диф-ю,наз интегрированием. Искомая ф-ция F(x) наз первообразной от ф-ции f(x).
Всякая непрерывная ф-ция f(x) имеет бесчисленное множество первообразных ф-ций которые отличаются друг от друг постоян слогаемыми,т.е. если F(x) первообразная от f(x),т.е.F`(x)=f(x) то и F(x)+c,где с-произвольная постоянная тоже первообразная от f(x) т.к. {F(x)+с}`=F`(x)-f(x)
Общее выражение F(x)+c в совокупности всех первообразных наз неопред интегралом от этой ф-ции f(x) и обозначается знаком ∫
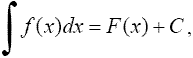
Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением
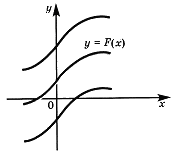
Геометрически.
Графики всех первообразных данной функции f (x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси Оу.
Свойство:
1)Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
2)Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
3) Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то
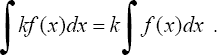
4)Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.
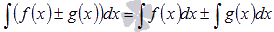
Таблица основных интегралов.
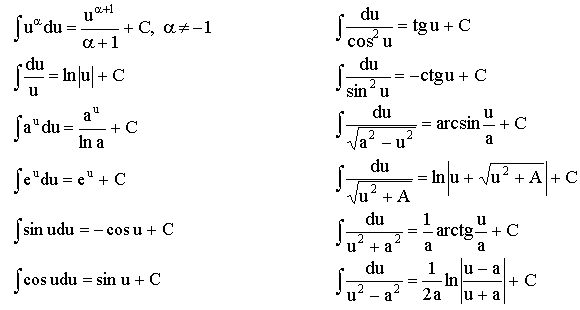
Вопрос 37.
Основные приемы интегрирования:подведение под знак дифференциала,замена переменной,интегрирование по частям.
1)непосредственное интегрирование-метод при котором данный интеграл путем тождественных преобразований подинтегральной ф-ции или выражений и примен св-в неопред интегр приводится к одному или нескольким табл интегралам.
2)замена переменной. Для нахождения интеграла ∫f(x)dx,заменяют перемен X новой переменной t связанной с X подходящей формулой,затем находят dx=ф`(t)dt
3)интегрирование по частям-из формулы дифференц произведения d(uv)=udv+vdu интегралов обеих ее частей uv=∫ udv+∫ vdu получается формула интегрирования по частям:
По этой формуле отыскание интеграла ∫ udv сводится к отысканию др интегр ∫ vdu и поэтому примен этой формулы целесообразно когда последний интеграл ∫ vdu проще исходного ∫udv за u чаще всего применяется ф-ция которая при деффер упрощается это обратные трионометр ф-ции(arcsin),логарифмет ф-ции(ln x)
Вопрос 38.
